Some words
“The more I get, the less I know.”
——bdim
Recently, I am trying to learn more about image recognition. One of the topics that I am interested in is LeNet, which is a classic convolutional neural network. In this article, I will try to re-implement a LeNet using PyTorch and then abstractly understand some parts that I do not quite understand. The contents of this article may be inaccurate and will continue to update the details. Welcome to discuss with me about this article.
LeNet5 is one of the earliest Convolutional Neural Networks (CNNs). It was proposed by Yann LeCun and others in 1998.
LeNet article links : Gradient-Based Learning Applied to Document Recognition.
The environment
My Macbook Pro M1 MAX:
c.' [email protected]
,xNMM. -----------------------------
.OMMMMo OS: macOS 14.5 23F79 arm64
lMM" Host: MacBookPro18,4
.;loddo:. .olloddol;. Kernel: 23.5.0
cKMMMMMMMMMMNWMMMMMMMMMM0: Uptime: 26 days, 21 hours, 14 mins
.KMMMMMMMMMMMMMMMMMMMMMMMWd. Packages: 275 (nix-user)
XMMMMMMMMMMMMMMMMMMMMMMMX. Shell: bash 5.2.26
;MMMMMMMMMMMMMMMMMMMMMMMM: Resolution: 3024x1964
:MMMMMMMMMMMMMMMMMMMMMMMM: DE: Aqua
.MMMMMMMMMMMMMMMMMMMMMMMMX. WM: Quartz Compositor
kMMMMMMMMMMMMMMMMMMMMMMMMWd. WM Theme: Blue (Dark)
'XMMMMMMMMMMMMMMMMMMMMMMMMMMk Terminal: Apple_Terminal
'XMMMMMMMMMMMMMMMMMMMMMMMMK. Terminal Font: Monaco
kMMMMMMMMMMMMMMMMMMMMMMd CPU: Apple M1 Max
;KMMMMMMMWXXWMMMMMMMk. GPU: Apple M1 Max
"cooc*" "*coo'" Memory: 24117MiB / 65536MiB
The software used
-
Python 3.11.9
-
PyTorch
You can install here Installing on macOS.
The network structure
Try to understand the structure of the network.
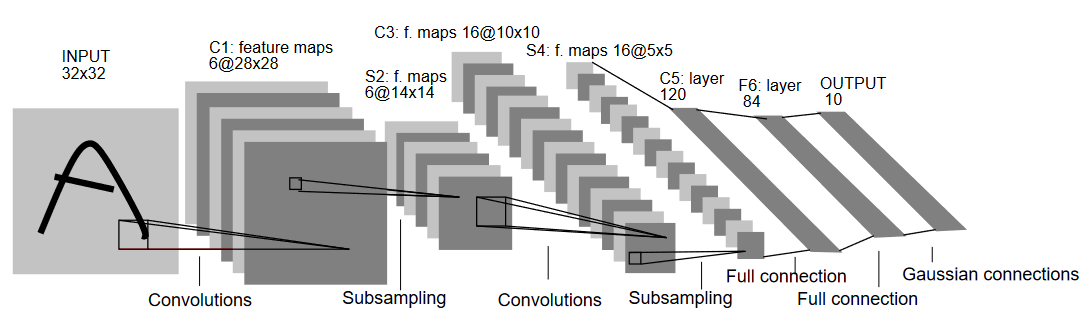
LeNet5 Architecture (Source: http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf)
Understanding the code
The code in this article is all available on the Github.
1. Installation
!pip3 install torch torchvision torchaudio
2. Inport modules and define the scalar
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
# Define the batch size, which is the number of samples that will be passed to the neural network during training.
batch_size = 64
# The "number" of classes is 10
num_classes = 10
# Define the learning rate, which is the size of the steps that will be taken in each iteration during training.
learning_rate = 0.001
# Define the number of epochs, which is the number of times that the entire dataset will be passed to the neural network.
num_epochs = 10
# Define the device, which is the hardware that will be used for training.
# If you are using a CPU-only machine, then you should use "cpu" instead of "mps".
# Or if you are using GPU-only machine, then you should use "cuda" instead of "mps".
device = torch.device('mps')
3. Imort the dataset from MINIST
# Load the MNIST dataset.
train_dataset = torchvision.datasets.MNIST(root = './data',
train = True, # Here means that we are loading the dateaset for training.
transform = transforms.Compose([ # Here we define the way of preprocessing the data.
transforms.Resize((32,32)), # Set the image to 32x32 pixels. The original MNIST images are 28x28 pixels. Here we increase their size to match the size of CIFAR-10 datasets for easier processing later on.
transforms.ToTensor(), # Convert the image to a tensor and scale its pixel values between [0, 1].
transforms.Normalize(mean = (0.1307,), std = (0.3081,))]), # Considering the MNIST dataset is a relatively small dataset, we also normalize its pixel values to have a mean of zero and standard deviation of one.
download = True)
test_dataset = torchvision.datasets.MNIST(root = './data',
train = False,
transform = transforms.Compose([
transforms.Resize((32,32)),
transforms.ToTensor(),
transforms.Normalize(mean = (0.1325,), std = (0.3105,))]),
download=True)
# Build a PyTorch DataLoader object that provides the ability to load and iterate over batches of training data.
# 'batch_size' set the number of samples in each batch, and'shuffle=True' means that the data will be reshuffled at every epoch end to increase randomness.
train_loader = torch.utils.data.DataLoader(dataset = train_dataset,
batch_size = batch_size,
shuffle = True)
test_loader = torch.utils.data.DataLoader(dataset = test_dataset,
batch_size = batch_size,
shuffle = True)
3.2 Discuss the Normalize Operation
Let’s talk about the Normalize deeper.
MNIST is a dataset of grayscale images, their pixel values are in the range 0 to 255. Gernerally, we want to normalize the data so that the mean value of each channel is zero and its standard deviation is one. They can use to be better for training and improve the accuracy.
transforms.Normalize(mean = (...), std = (...)) is a fonction that Pytorch provide, use to standerize the data. It will accept the two value, the mean and standard deviation of each channel. And here we pass the mean and standard deviation of MNIST.
Gernerally, when we compute the mean and standard deviation of each channel, we will use the following formula:
- mean:
mean = sum(pixels) / num_pixels - standard:
std = sqrt(sum((pixel - mean)^2) / num_pixels)
So, we can confirm the the different batch of MNIST have similar distribution. It is a common technique to train neural network and help the model converge faster and get better performance.
Normalize will do that:
normalized_image = (image - mean) / std
image is the pixel value of each image, and mean and std are the mean and standard deviation we provide. This transformation will scale all the features (in this case, the pixels) to a range with a mean of 0 and a standard deviation of 1.
It’s very imortant for training neural network, because the scale of features will affect the optimization algorithm. For example, if one feature’s range is 0 to 100 while another feature’s range is 0 to 1, the larger ranged feature will dominate the training process, because the optimization algorithm (such as gradient descent) will try to equally handle all features.
By standardization, we can confirm that the different batch of MNIST have similar distribution. It is a common technique to train neural network and help the model converge faster and get better performance.
4. Define the stacture of the model
class LeNet5(nn.Module):
def __init__(self, num_classes):
super(LeNet5, self).__init__()
self.layer1 = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=0),
nn.BatchNorm2d(6),
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2))
# self.layer1: The layer incude one Conv2d, one BatchNorm2d and one ReLU.
# BatchNorm2d use to normalize the 6 channels, activation function ReLU and max pooling(MaxPool2d, use the 2x2 window, stride is 2).
# On the first layer, we use the max pooling. There are some connmen ways to do the pooling, like average pooling、max pooling and K-max pooling.
# The max pooling: choose the maximum pixel in the sub-block of the input feature map as the maximum pooling
# The average pooling: choose the average pixel in the sub-block of the input feature map as the maximum pooling
# The K-max pooling: do the max pooling on each channel of the input feature map and then connect them together as
self.layer2 = nn.Sequential(
nn.Conv2d(6, 16, kernel_size=5, stride=1, padding=0),
nn.BatchNorm2d(16),
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2))
# BatchNorm2d use to normalize the 6 channels, activation function ReLU and max pooling(MaxPool2d, use the 2x2 window, stride is 2).
self.fc = nn.Linear(400, 120)
self.relu = nn.ReLU()
self.fc1 = nn.Linear(120, 84)
self.relu1 = nn.ReLU()
self.fc2 = nn.Linear(84, num_classes)
# Here we define the three fully connected layers (self.fc, self.fc1, self.fc2) and two ReLU activation functions.
# The fully-connected layers map the output of one layer into a specific dimension space for classification or regression tasks.
# Here, the first fully connected layer converts 400 features obtained from convolution and pooling operations to 120 features.
# The second fully connected layer converts the output of the first layer into a 84-dimensional space.
def forward(self, x):
out = self.layer1(x)
out = self.layer2(out)
out = out.reshape(out.size(0), -1)
out = self.fc(out)
out = self.relu(out)
out = self.fc1(out)
out = self.relu1(out)
out = self.fc2(out)
return out
# Here we define the way of forwarding the input data to compute the predicted results.
# It will pass the first layer and second layer to process the input data, then flattens the data into a one-dimensional vector (reshape operation).
# Then, it will pass the data through a fully connected layer, ReLU activation function and final prediction layer to compute the output.
5. Define the loss function and optimizer
# Here we create an instance of the LeNet5 model and move it to the device.
model = LeNet5(num_classes).to(device)
# Here we define the cross entropy loss function.
# The cross entropy loss measures the distance between two probability distributions p and q.
# According to the formula, the cross entropy loss is smaller when two probability distributions p and q are closer.
# Observed distribution p is close to the target distribution q.
cost = nn.CrossEntropyLoss()
# Here we define the Adam optimizer to update the model weights. The model.parameters() method returns an iterator over all learnable parameters of the model, and passes them to the optimizer.
# 'lr=learning_rate' Here we define the learning rate (lr), which is the size of the step taken by the optimizer to update the weights during training.
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
total_step = len(train_loader)
6. The training process of the model
total_step = len(train_loader)
for epoch in range(num_epochs):
for i, (images, labels) in enumerate(train_loader):
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
loss = cost(outputs, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (i+1) % 400 == 0:
print ('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'
.format(epoch+1, num_epochs, i+1, total_step, loss.item()))
Output:
Epoch [1/10], Step [400/938], Loss: 0.0907
Epoch [1/10], Step [800/938], Loss: 0.0916
Epoch [2/10], Step [400/938], Loss: 0.1063
Epoch [2/10], Step [800/938], Loss: 0.0360
Epoch [3/10], Step [400/938], Loss: 0.0459
Epoch [3/10], Step [800/938], Loss: 0.0269
Epoch [4/10], Step [400/938], Loss: 0.0539
Epoch [4/10], Step [800/938], Loss: 0.1063
Epoch [5/10], Step [400/938], Loss: 0.0020
Epoch [5/10], Step [800/938], Loss: 0.0347
Epoch [6/10], Step [400/938], Loss: 0.0048
Epoch [6/10], Step [800/938], Loss: 0.0082
Epoch [7/10], Step [400/938], Loss: 0.0537
Epoch [7/10], Step [800/938], Loss: 0.0012
Epoch [8/10], Step [400/938], Loss: 0.0043
Epoch [8/10], Step [800/938], Loss: 0.0006
Epoch [9/10], Step [400/938], Loss: 0.0003
Epoch [9/10], Step [800/938], Loss: 0.0004
Epoch [10/10], Step [400/938], Loss: 0.0794
Epoch [10/10], Step [800/938], Loss: 0.0179
6.2 Adam Optimizer
Adam is a common optimizer. It combines the advantages of momentum and RMSProp.
That is the result what I get after searching, is it like a mystery? Ha ha, I am too!
And someone told me that:
Adam use the momentum and adaptive learning rate to accelerate convergence. SGD-M add one order moment in SGD, AdaGrad and AdaDelta add two order moments (two order moment estimation) on SGD. Use both of them together is Adam - Adaptive + Momentum.
Here I read the 3.3.3 chapter of Professor Li’s deep learning course. The first two small chapters are about Adaptive Learning Rate. Then, I read the AdaGrad and RMSProp algorithms. The third small chapter is about Adam optimizer.
We should first understand what momentum is. I am not very clear that before.
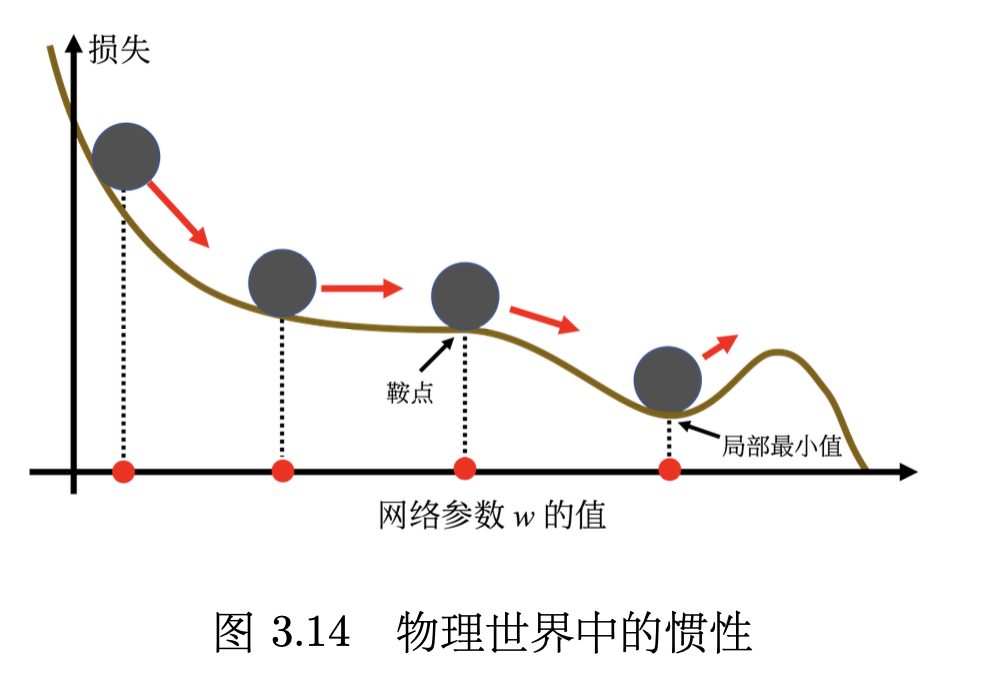
动量法(momentum method)是另外一个可以对抗鞍点或局部最小值的方法。如图 3.14 所示,假设误差表面就是真正的斜坡,参数是一个球,把球从斜坡上滚下来,如果使用梯度下降,球走到局部最小值或鞍点就停住了。 但是在物理的世界里,一个球如果从高处滚下来,就算滚到鞍点或鞍点,因为惯性的关系它还是会继续往前走。如果球的动量足够大,其甚至翻过小坡继续往前走。 因此在物理的世界里面,一个球从高处滚下来的时候,它并不一定会被鞍点或局部最小值卡住,如果将其应用到梯度下降中,这就是动量。
——《深度学习教程》
引入动量后,可以从两个角度来理解动量法。一个角度是动量是梯度的负反方向加上前一次移动的方向。另外一个角度是当加上动量的时候,更新的方向不是只考虑现在的梯度,而是考虑过去所有梯度的总和。
——《深度学习教程》
动量的简单例子如图 3.17 所示。红色表示负梯度方向,蓝色虚线表示前一步的方向,蓝色实线表示真实的移动量。一开始没有前一次更新的方向,完全按照梯度给指示往右移动参数。负梯度方向跟前一步移动的方向加起来,得到往右走的方向。一般梯度下降走到一个局部最小值或鞍点时,就被困住了。但有动量还是有办法继续走下去,因为动量不是只看梯度, 还看前一步的方向。即使梯度方向往左走,但如果前一步的影响力比梯度要大,球还是有可能继续往右走,甚至翻过一个小丘,也许可以走到更好的局部最小值,这就是动量有可能带来的好处。
——《深度学习教程》
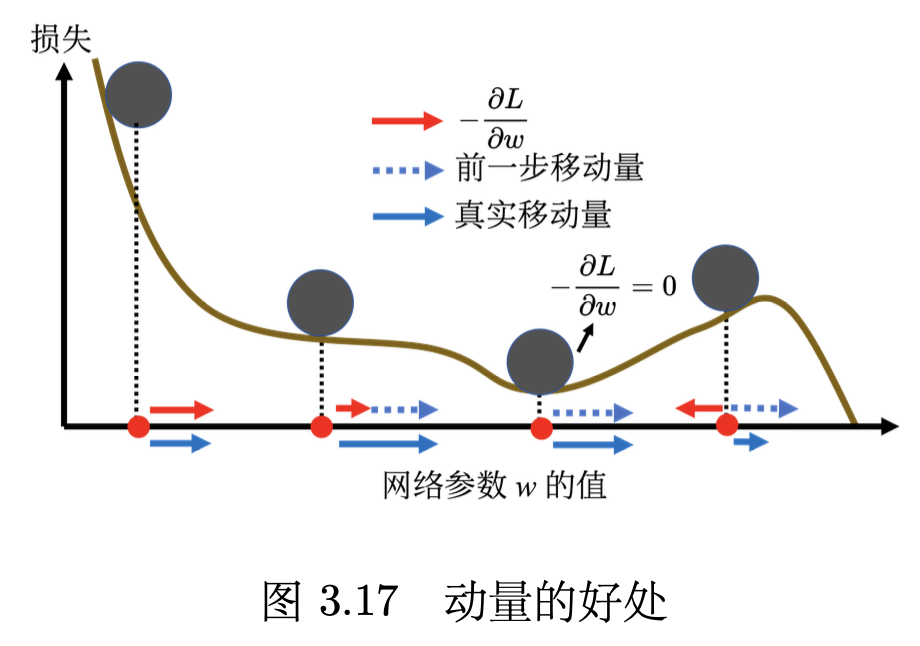
The course use the physical angle to understand momentum, it is so beautiful. Here we can understand momentum concept very well. The sum of past gradients is like a force that push the whole model forward. And the momentum is just a kind of acceleration. So, use momentum, we can make the learning rate more stable and converge faster.
我们现在训练一个网络,训练到现在参数在临界点附近,再根据特征值的正负号判断该临界点是鞍点还是局部最小值。实际上在训练的时候,要走到鞍点或局部最小值,是一件困难的事情。一般的梯度下降,其实是做不到的。用一般的梯度下降训练,往往会在梯度还很大的时候,损失就已经降了下去,这个是需要特别方法训练的。要走到一个临界点其实是比较困难的,多数时候训练在还没有走到临界点的时候就已经停止了。
——《深度学习教程》
最原始的梯度下降连简单的误差表面都做不好,因此需要更好的梯度下降的版本。在梯度下降里面,所有的参数都是设同样的学习率,这显然是不够的,应该要为每一个参数定制化学习率,即引入自适应学习率(adaptive learning rate)的方法,给每一个参数不同的学习率。
——《深度学习教程》
Here we can find that, the different from SGD, Adam is more like a combination of SGD and Momentum. It uses momentum to accelerate the convergence, but also use the learning rate decay to avoid the oscillation.
AdaGrad(Adaptive Gradient)是典型的自适应学习率方法,其能够根据梯度大小自动调整学习率。AdaGrad 可以做到梯度比较大的时候,学习率就减小,梯度比较小的时候,学习率就放大。
——《深度学习教程》
The way of the AdaGrad let me think that, the AdaGrad is a method to adjust the learning rate. But it can’t solve the problem that, the different gradient use different learning rate. So, there is another way to solve this problem.
AdaGrad 在算均方根的时候,每一个梯度都有同等的重要性,但在 RMSprop 里面,可以自己调整现在的这个梯度的重要性。
——《深度学习教程》
We can get that: RMSprop has a important feature, which is that it can adjust the learning rate.
最常用的优化的策略或者优化器(optimizer)是Adam(Adaptive moment estima- tion)。Adam 可以看作 RMSprop 加上动量,其使用动量作为参数更新方向,并且能够自适应调整学习率。PyTorch 里面已经写好了 Adam 优化器,这个优化器里面有一些超参数需要人为决定,但是往往用 PyTorch 预设的参数就足够好了。
——《深度学习教程》
Theblogintroduce the some advantages of Adam :
- Adaptive learning rates: Adam computes individual learning rates for each parameter, speeding up convergence and improving the quality of the final solution.
- Suitable for noisy gradients: Adam performs well in cases with noisy gradients, such as training deep learning models with mini-batches.
- Low memory requirements: Adam requires only two additional variables for each parameter, making it memory-efficient.
- Robust to the choice of hyperparameters: Adam is relatively insensitive to the choice of hyperparameters, making it easy to use in practice.
Testing the model
with torch.no_grad():
correct = 0
total = 0
for images, labels in test_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: {} %'.format(100 * correct / total))
Output:
Accuracy of the network on the 10000 test images: 98.96 %
Summarize
LeNet is a very classic convolutional neural network, first published in 1989. It is a good starting point for deep learning. After research the deatils of the model, I get a lot of knowledge about the model. But I only reimplement LeNet 5, there are many details that are not included in the original paper.
Thanks for reading this article, if you have any questions or suggestions, please email me.
Reference
https://pytorch.org/get-started/locally/
https://blog.paperspace.com/writing-lenet5-from-scratch-in-python/
http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf?ref=blog.paperspace.com
https://paddlepedia.readthedocs.io/en/latest/tutorials/deep_learning/loss_functions/CE_Loss.html