讲几句废话
“当我以为自己掌握了大量知识的时候,才发现自己所知道的只是这个领域中的沧海一粟。”
——bdim 学习感悟
最近一直在尝试学习图像识别相关的内容,其中就有 LeNet 这个经典的卷积神经网络,在这里记录一下学习过程。经过重复阅读 《深度学习图解》 这本书之后,终于能够理解 Lenet 的大部分细节。在这里我尝试通过自己的理解,尝试重新实现一个 LeNet,并通过查询资料将一些自己不是太理解的内容也来抽象理解一下,本文内容可能并不准确,并将持续更新细节。欢迎对本文提出质疑并与作者进行交流学习!!
LeNet5 is one of the earliest Convolutional Neural Networks (CNNs). It was proposed by Yann LeCun and others in 1998.
LeNet 论文链接 : Gradient-Based Learning Applied to Document Recognition.
环境
我使用的设备环境:
c.' [email protected]
,xNMM. -----------------------------
.OMMMMo OS: macOS 14.5 23F79 arm64
lMM" Host: MacBookPro18,4
.;loddo:. .olloddol;. Kernel: 23.5.0
cKMMMMMMMMMMNWMMMMMMMMMM0: Uptime: 26 days, 21 hours, 14 mins
.KMMMMMMMMMMMMMMMMMMMMMMMWd. Packages: 275 (nix-user)
XMMMMMMMMMMMMMMMMMMMMMMMX. Shell: bash 5.2.26
;MMMMMMMMMMMMMMMMMMMMMMMM: Resolution: 3024x1964
:MMMMMMMMMMMMMMMMMMMMMMMM: DE: Aqua
.MMMMMMMMMMMMMMMMMMMMMMMMX. WM: Quartz Compositor
kMMMMMMMMMMMMMMMMMMMMMMMMWd. WM Theme: Blue (Dark)
'XMMMMMMMMMMMMMMMMMMMMMMMMMMk Terminal: Apple_Terminal
'XMMMMMMMMMMMMMMMMMMMMMMMMK. Terminal Font: Monaco
kMMMMMMMMMMMMMMMMMMMMMMd CPU: Apple M1 Max
;KMMMMMMMWXXWMMMMMMMk. GPU: Apple M1 Max
"cooc*" "*coo'" Memory: 24117MiB / 65536MiB
我的软件环境
- Python3
我使用的 Python 版本是 3.11.9 。
- PyTorch
参考 PyTorch 官网的链接进行安装 Installing on macOS
图解 LeNet
首先来简单通过图示来了解一下这个 LeNet 网络的结构。
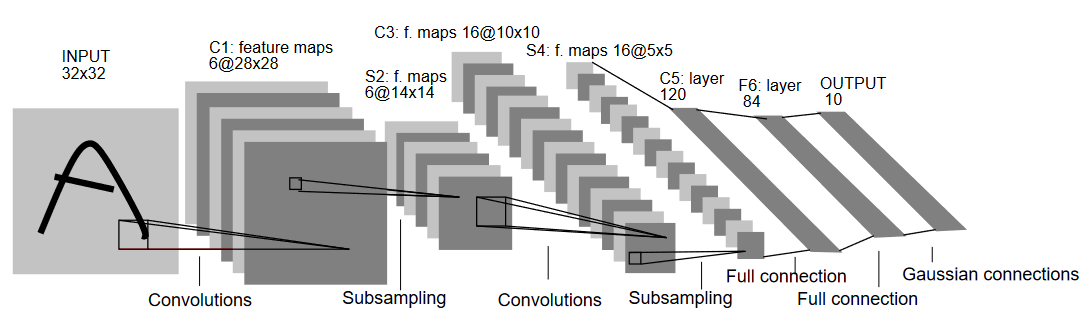
LeNet5 Architecture (Source: http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf)
代码理解
本文以下的代码内容都是通过 jupyter Notebook 来进行展示的, 可以按照顺序将代码内容复制到 Jupyter Notebook 中运行。本文所有代码也已经上传至仓库 https://github.com/bdim404/LeNet-5 。
1. 安装相关库
!pip3 install torch torchvision torchaudio
2. 导入相关库并定义网络的关键标量。
import torch
import torch.nn as nn
import torchvision
import torchvision.transforms as transforms
# 定义批量大小为64,这是在训练过程中每次传递给神经网络的样本数量
batch_size = 64
# 数字的种类数量为10
num_classes = 10
# 定义学习率为0.001
learning_rate = 0.001
# 定义训练轮数为10,这意味着整个数据集将被传递给神经网络10次
num_epochs = 10
# 定义了将在 Apple 设备使用 GPU 进行训练
device = torch.device('mps')
3. 导入 MINIST 数据集
# 加载 MNIST 数据集
train_dataset = torchvision.datasets.MNIST(root = './data',
train = True, # '表示我们需要加载训练数据集
transform = transforms.Compose([ # transform 的作用是定义了对图像进行预处理的方式
transforms.Resize((32,32)), # 将图像大小调整为32x32像素。原始MNIST图像是28x28像素,这里我们将其增加到与CIFAR-10数据集相同的尺寸以方便后续处理
transforms.ToTensor(), # 将图像转换为PyTorch Tensor格式,并将像素值缩放到[0, 1]之间
transforms.Normalize(mean = (0.1307,), std = (0.3081,))]), # 标准化图像数据。这里使用了MNIST训练和测试集的均值和标准差,以确保数据在不同的批次中有相似的分布。
download = True)
test_dataset = torchvision.datasets.MNIST(root = './data',
train = False,
transform = transforms.Compose([
transforms.Resize((32,32)),
transforms.ToTensor(),
transforms.Normalize(mean = (0.1325,), std = (0.3105,))]),
download=True)
# 创建了一个PyTorch DataLoader对象,它提供了从训练数据集中按批加载和迭代数据的功能。
# 'batch_size'参数指定每个批次包含多少样本,'shuffle=True'表示在每个时期结束时重新排列数据以增加随机性。
train_loader = torch.utils.data.DataLoader(dataset = train_dataset,
batch_size = batch_size,
shuffle = True)
test_loader = torch.utils.data.DataLoader(dataset = test_dataset,
batch_size = batch_size,
shuffle = True)
3.2 讨论一下我并不是非常理解的地方
让我们更深入地讨论 Normalize 操作。
MNIST数据集是灰度图像数据,其像素值范围从0(黑色)到255(白色)。通常在训练神经网络时,将输入特征标准化到均值为0、标准差为1的分布中会有益处。这样可以使得模型更容易地学习并收敛。
transforms.Normalize(mean = (...), std = (...))是PyTorch提供的一个函数,用于标准化输入数据。它接受两个参数:均值和标准差。在这段代码中,我们传递了MNIST训练集的均值和标准差(分别为0.1307和0.3081)。
均值和标准差通常是根据训练数据集计算得出的统计量。在上述代码中,提供了MNIST训练集的均值(0.1307)和标准差(0.3081)。
这些值用于标准化训练和测试数据集,以使它们具有相似的分布。在实践中,计算这些值通常是在加载数据之前完成的,因为我们希望确保测试数据集与训练数据集具有相同的统计属性(即,均值和标准差)。
计算这些值时,一般会将所有训练样本的像素值组合成一个向量,并对其进行如下计算:
- 均值:
mean = sum(pixels) / num_pixels - 标准差:
std = sqrt(sum((pixel - mean)^2) / num_pixels)
这样,我们可以确保训练和测试数据集在不同批次中具有相似的分布。使用正确计算的均值和标准差对输入进行标准化是神经网络训练的一种常见技术,它有助于模型更快地收敛并获得较好的性能。
Normalize操作对图像数据进行以下转换:
normalized_image = (image - mean) / std
其中,‘image’是原始图像的每个像素值,‘mean’和’std’分别是我们提供的均值和标准差。这样的转换将数据集的所有特征(在这种情况下是像素)缩放到均值为0、标准差为1的范围内。
这个操作对于训练模型非常重要,因为不同特征的尺度可能会对优化算法产生负面影响。例如,如果一个特征的范围在0到100,而另一个特征的范围在0到1,那么具有更大范围的特征将对训练过程起主导作用,因为优化算法(如梯度下降)会尝试平等地处理所有特征。
通过标准化数据集,我们可以确保每个特征在优化期间都被考虑到相同程度,从而使模型更容易学习并提高其性能。这也有助于加速训练过程。
4. 定义网络结构
class LeNet5(nn.Module):
def __init__(self, num_classes):
super(LeNet5, self).__init__()
self.layer1 = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=0),
nn.BatchNorm2d(6),
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2))
# self.layer1: 这是一个包含多个层次操作的序列,包括卷积层(Conv2d,输入通道为1,输出通道为6,使用5x5的卷积核,步幅为1, 并将空余的部分使用 0 来填充)
# 批归一化层(BatchNorm2d,对6个通道进行批处理归一化)、激活函数ReLU和最大池化层(MaxPool2d,使用2x2的池化窗口,步幅为2)。
# 在本层中,我们使用的池化方式是最大池化方式。池化的几种常见方法包括:平均池化、最大池化、K-max池化。
# 最大池化: 从输入特征图的某个区域子块中选择值最大的像素点作为最大池化结果。
# 平均池化: 从输入特征图的某个区域子块中选择值平均的像素点作为最大池化结果。
# K-max池化: 在K个通道上进行最大池化,然后将每个通道上的最大池化结果连接起来作为输出。
self.layer2 = nn.Sequential(
nn.Conv2d(6, 16, kernel_size=5, stride=1, padding=0),
nn.BatchNorm2d(16),
nn.ReLU(),
nn.MaxPool2d(kernel_size = 2, stride = 2))
# self.layer2: 这是第二个包含多个层次操作的序列,类似于前一层但是输入通道数变成了6(因为上一层有6个输出通道),而输出通道数变成了16。
self.fc = nn.Linear(400, 120)
self.relu = nn.ReLU()
self.fc1 = nn.Linear(120, 84)
self.relu1 = nn.ReLU()
self.fc2 = nn.Linear(84, num_classes)
# 接下来定义了三个全连接层(self.fc, self.fc1, self.fc2)和两个ReLU激活函数。
# 全连接层用于将前一层的输出映射到一个特定维度的空间,以便进行分类或回归任务。
# 这里,第一个全连接层将400个特征(由卷积和池化操作得来)转换为120个特征,
# 第二个将120个特征转换为84个特征,最后的全连接层将84个特征映射到指定数量的类别上(这就是num_classes参数)
def forward(self, x):
out = self.layer1(x)
out = self.layer2(out)
out = out.reshape(out.size(0), -1)
out = self.fc(out)
out = self.relu(out)
out = self.fc1(out)
out = self.relu1(out)
out = self.fc2(out)
return out
# forward方法定义了前向传播过程,即如何使用输入数据来计算模型的预测结果。
# 它首先通过第一层和第二层处理输入数据,然后将这些数据展平成一个一维向量(reshape操作),
# 接着通过全连接层、ReLU激活函数以及最终的预测层计算输出。
4.1 让我们来聊聊卷积神经网络
在我的理解看来,卷积神经网络的核心思想是通过将输入图像分解为多个特征图(feature map),然后在每个特征图中学习不同的过滤器(filter)。
他还有以下特点:
- 局部连接(local connection):
卷积层的输出特征中的每一个元素都只和上一层特征对应位置的局部邻域内的元素相连,构成一个局部连接网络。
- 参数共享(parameter sharing):
卷积层的每一个卷积核在特征的不同位置上是共享参数的。参数共享能够进一步减少卷积层的参数量,此时每一个卷积核可以提取具有某种固定模式的特征(比如水平线段或竖直线段),通过使用复数个卷积核能够提取不同语义信息的特征。
- 平移不变性(translation invariance):
平移变换是指把一幅图像或一个空间中的每一个点沿相同方向移动相同的距离。平移等变性是指对输入进行平移变换时,系统在不同位置的工作原理相同,但它的响应随着目标位置的变化而变化。对于卷积层,输入图像经过平移后,输出特征图上的对应特征表达也是平移的。
滤波器就是一个一个的张量,这些张量里面的数值就是模型里面的参数。这些滤波器里面的数值其实是未知的,它是可以通过学习找出来的。
——《深度学习教程》
5. 定义损失函数和优化器
# 创建了一个 LeNet5 模型的实例,并将其移动到了设备上。
model = LeNet5(num_classes).to(device)
# 这里定义了损失函数为交叉熵损失(cross-entropy loss)
# 交叉熵刻画了两个概率分布之间的距离,旨在描绘通过概率分布 𝑞 来表达概率分布 𝑝 的困难程度。
# 根据公式不难理解,交叉熵越小,两个概率分布 𝑝 和 𝑞 越接近。
# 很显然,一个良好的神经网络要尽量保证对于每一个输入数据,
# 神经网络所预测类别分布概率与实际类别分布概率之间的差距越小越好,即交叉熵越小越好。
# 于是,可将交叉熵作为损失函数来训练神经网络。
cost = nn.CrossEntropyLoss()
# 这里使用 Adam 优化器来更新模型的权重。model.parameters() 返回模型中所有可学习参数的迭代器,并将它们传递给优化器。
# lr=learning_rate 指定了学习率(learning rate),即每次更新权重时移动的步长大小。
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
# 这行代码计算训练数据加载器中的样本数量,以便在训练过程中可以知道剩余的步骤数
total_step = len(train_loader)
6. 训练模型
total_step = len(train_loader)
for epoch in range(num_epochs):
# 在当前时期内,循环遍历训练数据加载器中的每个批次(即一组图像和相应的标签。
# enumerate()函数用于跟踪当前的批次索引i。
for i, (images, labels) in enumerate(train_loader):
images = images.to(device)
labels = labels.to(device)
#对模型传递当前批次的图像并获得预测输出。
# 向前传播
outputs = model(images)
loss = cost(outputs, labels)
# 清除优化器中累积的梯度。在执行反向传播之前,这很重要,因为默认情况下PyTorch会累加梯度。
optimizer.zero_grad()
# 反向传播
loss.backward()
# 使用计算出的梯度更新模型的参数。
optimizer.step()
# 每 400 批次打印输出一次当前的进度信息。
if (i+1) % 400 == 0:
print ('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'
.format(epoch+1, num_epochs, i+1, total_step, loss.item()))
训练输出:
Epoch [1/10], Step [400/938], Loss: 0.0907
Epoch [1/10], Step [800/938], Loss: 0.0916
Epoch [2/10], Step [400/938], Loss: 0.1063
Epoch [2/10], Step [800/938], Loss: 0.0360
Epoch [3/10], Step [400/938], Loss: 0.0459
Epoch [3/10], Step [800/938], Loss: 0.0269
Epoch [4/10], Step [400/938], Loss: 0.0539
Epoch [4/10], Step [800/938], Loss: 0.1063
Epoch [5/10], Step [400/938], Loss: 0.0020
Epoch [5/10], Step [800/938], Loss: 0.0347
Epoch [6/10], Step [400/938], Loss: 0.0048
Epoch [6/10], Step [800/938], Loss: 0.0082
Epoch [7/10], Step [400/938], Loss: 0.0537
Epoch [7/10], Step [800/938], Loss: 0.0012
Epoch [8/10], Step [400/938], Loss: 0.0043
Epoch [8/10], Step [800/938], Loss: 0.0006
Epoch [9/10], Step [400/938], Loss: 0.0003
Epoch [9/10], Step [800/938], Loss: 0.0004
Epoch [10/10], Step [400/938], Loss: 0.0794
Epoch [10/10], Step [800/938], Loss: 0.0179
6.2 Adam 优化器
这里我们讨论一下 Adam 优化器。
Adam 是一种常用的优化器,它结合了动量(momentum)和 RMSProp 的优点。
这是我搜索之后大家都这么告诉我的,是不是看起来一头雾水?哈哈,我也是!
还有这样解释的:
Adam使用动量和自适应学习率来加快收敛速度。SGD-M在SGD基础上增加了一阶动量,AdaGrad和AdaDelta在SGD基础上增加了二阶动量(二阶矩估计)。把一阶动量和二阶动量都用起来,就是Adam了——Adaptive + Momentum。
这里我阅读了 李宏毅老师的 《深度学习教程》3.3.3 章节。前两个小章节是介绍了 自适应学习率 是什么,然后介绍了 AdaGrad 和 RMSProp 两种常用的自适应学习率算法。第三个小章节是介绍了 Adam 优化器。
因为我只是深度学习的初学者,对于 Adam 优化器不太了解,在阅读 《深度学习图解》 这本书里只是了解了几种不同的梯度下降的方法。对于不同学习率的设定也是一头雾水,总是一概认为越小的学习率越好,但实际上并不是这样的。
不过我觉得我需要先了解一下什么是动量(momentum)。因为我之前不太明白什么是动量。
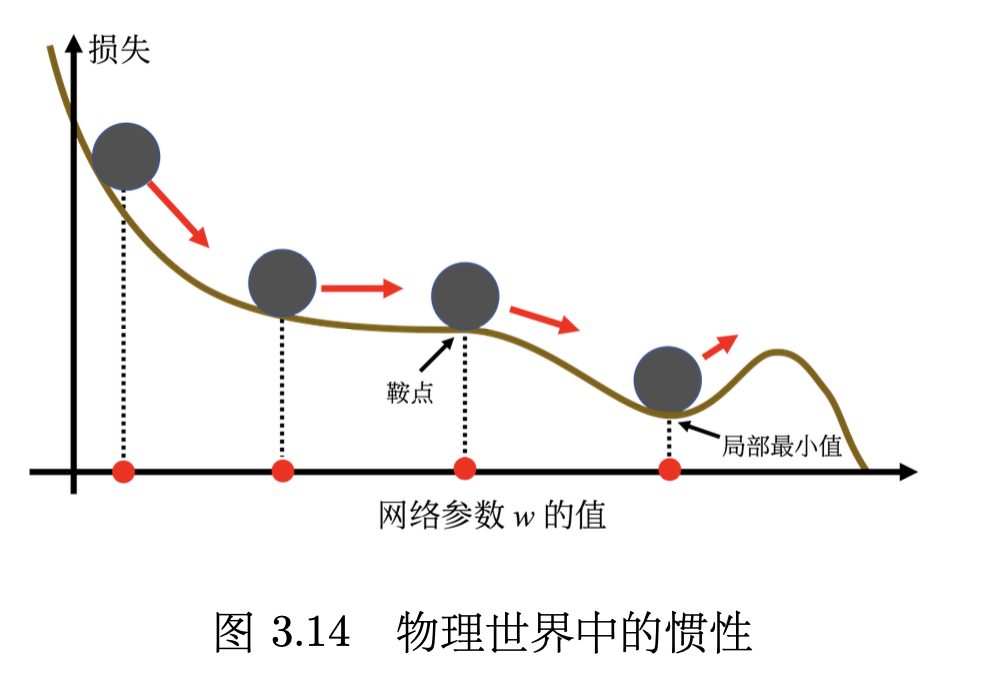
动量法(momentum method)是另外一个可以对抗鞍点或局部最小值的方法。如图 3.14 所示,假设误差表面就是真正的斜坡,参数是一个球,把球从斜坡上滚下来,如果使用梯度下降,球走到局部最小值或鞍点就停住了。 但是在物理的世界里,一个球如果从高处滚下来,就算滚到鞍点或鞍点,因为惯性的关系它还是会继续往前走。如果球的动量足够大,其甚至翻过小坡继续往前走。 因此在物理的世界里面,一个球从高处滚下来的时候,它并不一定会被鞍点或局部最小值卡住,如果将其应用到梯度下降中,这就是动量。
——《深度学习教程》
引入动量后,可以从两个角度来理解动量法。一个角度是动量是梯度的负反方向加上前一次移动的方向。另外一个角度是当加上动量的时候,更新的方向不是只考虑现在的梯度,而是考虑过去所有梯度的总和。
——《深度学习教程》
动量的简单例子如图 3.17 所示。红色表示负梯度方向,蓝色虚线表示前一步的方向,蓝色实线表示真实的移动量。一开始没有前一次更新的方向,完全按照梯度给指示往右移动参数。负梯度方向跟前一步移动的方向加起来,得到往右走的方向。一般梯度下降走到一个局部最小值或鞍点时,就被困住了。但有动量还是有办法继续走下去,因为动量不是只看梯度, 还看前一步的方向。即使梯度方向往左走,但如果前一步的影响力比梯度要大,球还是有可能继续往右走,甚至翻过一个小丘,也许可以走到更好的局部最小值,这就是动量有可能带来的好处。
——《深度学习教程》
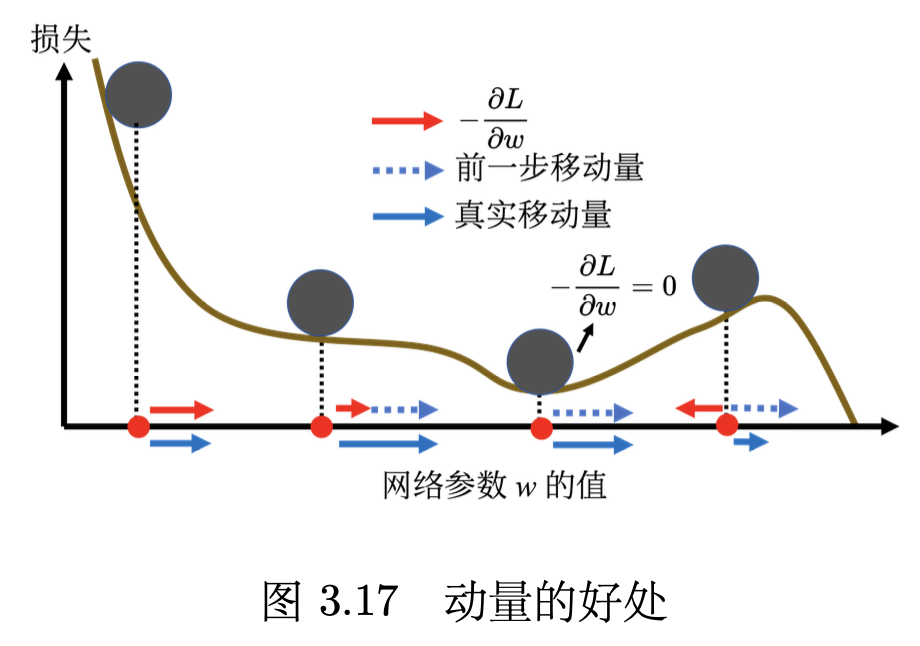
这里通过物理的角度来理解动量,实在是太形象了,这里我们就可以很好地理解动量这个概念。过去梯度的总和像一个力推动着整个模型向前推进。
我们现在训练一个网络,训练到现在参数在临界点附近,再根据特征值的正负号判断该临界点是鞍点还是局部最小值。实际上在训练的时候,要走到鞍点或局部最小值,是一件困难的事情。一般的梯度下降,其实是做不到的。用一般的梯度下降训练,往往会在梯度还很大的时候,损失就已经降了下去,这个是需要特别方法训练的。要走到一个临界点其实是比较困难的,多数时候训练在还没有走到临界点的时候就已经停止了。
——《深度学习教程》
最原始的梯度下降连简单的误差表面都做不好,因此需要更好的梯度下降的版本。在梯度下降里面,所有的参数都是设同样的学习率,这显然是不够的,应该要为每一个参数定制化学习率,即引入自适应学习率(adaptive learning rate)的方法,给每一个参数不同的学习率。
——《深度学习教程》
也就是说,针对不同的梯度下降,也要有不同的学习率,这样才能更好地去适应不同的梯度。
AdaGrad(Adaptive Gradient)是典型的自适应学习率方法,其能够根据梯度大小自动调整学习率。AdaGrad 可以做到梯度比较大的时候,学习率就减小,梯度比较小的时候,学习率就放大。
——《深度学习教程》
这一个方法让我眼前一亮,这样不就能很好地解决不同梯度下使用不同学习率的问题了吗?哦不,还有更好的方法,针对不同梯度下使用不同的学习率的问题,还有一种方法叫做 RMSprop 。
AdaGrad 在算均方根的时候,每一个梯度都有同等的重要性,但在 RMSprop 里面,可以自己调整现在的这个梯度的重要性。
——《深度学习教程》
而 RMSprop 的一个重要特点是它可以自己调整现在的这个梯度的重要性。
最常用的优化的策略或者优化器(optimizer)是Adam(Adaptive moment estima- tion)。Adam 可以看作 RMSprop 加上动量,其使用动量作为参数更新方向,并且能够自适应调整学习率。PyTorch 里面已经写好了 Adam 优化器,这个优化器里面有一些超参数需要人为决定,但是往往用 PyTorch 预设的参数就足够好了。
——《深度学习教程》
这篇博客介绍了 Adam 的一些优势:
- Adaptive learning rates: Adam computes individual learning rates for each parameter, speeding up convergence and improving the quality of the final solution.
- Suitable for noisy gradients: Adam performs well in cases with noisy gradients, such as training deep learning models with mini-batches.
- Low memory requirements: Adam requires only two additional variables for each parameter, making it memory-efficient.
- Robust to the choice of hyperparameters: Adam is relatively insensitive to the choice of hyperparameters, making it easy to use in practice.
简单来说就是,鲁棒性好、适应能力强(不挑剔)、内存资源占用低。 是娱乐休闲、家居旅行、工作学习的不二之选。
当然,《深度学习教程》这本书里提供了更加详细的数学公式推导和讲解,如果需要了解地更加细致,建议去阅读原文。
测试
# 在测试集上评估模型的性能。
# with torch.no_grad(): - 这一行表示在以下代码块中,不需要计算梯度。
# 这是因为测试阶段只关注模型的性能,而不需要进行反向传播和权重更新。
with torch.no_grad():
# 初始化了用于计算模型准确率的变量:
# correct跟踪预测正确的样本数,
# 而total是数据集中总样本数。
correct = 0
total = 0
for images, labels in test_loader:
images = images.to(device)
labels = labels.to(device)
outputs = model(images) # 使用测试模型对当前批次的图像进行预测。
_, predicted = torch.max(outputs.data, 1) # 从模型输出中获取预测类别,即具有最高得分的类别。
total += labels.size(0)
correct += (predicted == labels).sum().item()
print('Accuracy of the network on the 10000 test images: {} %'.format(100 * correct / total))
测试输出:
Accuracy of the network on the 10000 test images: 98.96 %
总结
LeNet 作为一个非常经典的卷积神经网络,在 20 世纪 90 年代初期就已经被提出。它是第一个成功应用深度学习的人工智能模型。而在现在,对于我们这些初学者,里面有非常多的细节值得去深究。不过我们本次复现的是 LeNet 5 ,中间有很多技术内容都是都是近几年才提出的,他们的加入让 LeNet 变得更加强大。
参考链接
https://pytorch.org/get-started/locally/
https://0809zheng.github.io/2020/03/06/CNN.html
https://blog.paperspace.com/writing-lenet5-from-scratch-in-python/
http://yann.lecun.com/exdb/publis/pdf/lecun-01a.pdf?ref=blog.paperspace.com
https://paddlepedia.readthedocs.io/en/latest/tutorials/deep_learning/loss_functions/CE_Loss.html