原视频: The spelled-out intro to language modeling: building makemore
注意,可以透过将代码复制到 colab 或 jupyter notebook 运行, 部分生图的输出结果本文贴图效果不佳,所以建议亲自动手跟着视频操作理解。本文的笔记仅作参考。
目标
Makemore 接收一个文本文件(例如提供的 names.txt),其中每一行都假定为一个训练“对象”。
然后,它生成更多类似的东西。
在内部,Makemore 是一个字符级语言模型。每一行都包含一个示例,即模型中的一系列单个字符。
这是Makemore操作的层面,试图预测序列/单词中的下一个字符。
Makemore 是一个以现代方式实现的字符级语言建模工具。
我们的目标是从零开始构建Makemore,并理解其工作原理。
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt
%matplotlib inline
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") # Use GPU if available (faster calculations with PyTorch)
words = open('names.txt', 'r').read().splitlines() #Python list of strings
print("First 10 names: ", words[:10]) # First ten names, each as separate string
print("Dataset size: ", len(words)) # Amount of words in dataset
print("Shortest name: ", min(len(w) for w in words)) # Smallest word in dataset
print("Longest name: ", max(len(w) for w in words)) # Longest word in dataset
First 10 names: ['emma', 'olivia', 'ava', 'isabella', 'sophia', 'charlotte', 'mia', 'amelia', 'harper', 'evelyn']
Dataset size: 32033
Shortest name: 2
Longest name: 15
采用字符级方法,每个单词实际上是一组打包的示例,这些示例说明了哪个字符跟在哪个字符后面 / 哪个字符先出现 / 字符序列中大概有多少字符。
二元语言模型
二元语言建模方法一次处理两个给定的字符。
它实际上只作用于这些局部的、小规模的结构,有效地忽略了字符序列/名称中可能存在的更多信息。
这是一个很好的起点。
for w in words[:1]:
chs = ['<S>'] + list(w) + ['<E>']
for ch1, ch2 in zip(chs, chs[1:]): # Neat way for two char 'sliding-window'
print(ch1, ch2)
<S> e
e m
m m
m a
a <E>
对于 “emma”,这会返回 <S>e, em, mm, ma, a<E>。
一个模型现在可能会推断出 m 很可能跟随 e 出现,a 很可能用来结束一个单词,等等。
请注意,<S> 和 <E> 是我们添加的特殊字符,用来标记单词的开始和结束,
这样非常明确地为每个开始和结束字符添加了额外的字符对信息。
获取哪些字符跟随哪些字符的统计数据的最简单方法就是计算训练集中出现的组合。
为此我们需要一个字典。
b = {}
for w in words:
chs = ['<S>'] + list(w) + ['<E>']
for ch1, ch2 in zip(chs, chs[1:]): # Neat way for two char 'sliding-window'
bigram = (ch1, ch2) # bigram is the (ch1, ch2) tupel
b[bigram] = b.get(bigram, 0) + 1 # If tupel count not ex. -> 0 + 1
字典 b 包含了整个数据集中字母组合的累积/统计信息。让我们来深入了解一下。
# b.items() returns tupels like (('<S>', a), 34)
# sorted() would sort items by tupel, not amount
# to sort by amount: lambda function replaces key with value (amount) high->low
sorted(b.items(), key = lambda keyvalue: -keyvalue[1])
[(('n', '<E>'), 6763),
(('a', '<E>'), 6640),
(('a', 'n'), 5438),
(('<S>', 'a'), 4410),
(('e', '<E>'), 3983),
(('a', 'r'), 3264),
(('e', 'l'), 3248),
(('r', 'i'), 3033),
(('n', 'a'), 2977),
(('<S>', 'k'), 2963),
(('l', 'e'), 2921),
(('e', 'n'), 2675),
(('l', 'a'), 2623),
(('m', 'a'), 2590),
(('<S>', 'm'), 2538),
(('a', 'l'), 2528),
(('i', '<E>'), 2489),
(('l', 'i'), 2480),
(('i', 'a'), 2445),
(('<S>', 'j'), 2422),
(('o', 'n'), 2411),
(('h', '<E>'), 2409),
(('r', 'a'), 2356),
(('a', 'h'), 2332),
(('h', 'a'), 2244),
...
(('j', 'b'), 1),
(('x', 'm'), 1),
(('w', 'g'), 1),
(('t', 'b'), 1),
(('z', 'x'), 1)]
Output is truncated. View as a scrollable element or open in a text editor. Adjust cell output settings...
例如,通过这种方式找到的最可能的组合是 (('n', '<E>'), 6763)。
实际上,将这些信息保存在一个二维数组中,而不是字典中,会更加方便。
这样,我们可以在保持统一结构的同时,轻松访问字符对的出现次数。
因此,我们应该构建这样一个矩阵/表格,使得
- 行是第一个字符,
- 列是第二个字符。
在这个表中,一个单元格包含每行和每列的出现次数。
对于数据处理和处理,我们使用 PyTorch。
我们有 26 个字母 +2 个特殊字符。这构成了一个 \(28\times 28\) 的数组。
N = torch.zeros((28,28), dtype=torch.int32) # datatype would otherwise be float32 by default
# Problem: We'll have only chars, but below we index using ints -> Need for mapping
chars = sorted(list(set(''.join(words)))) # set(): Throwing out letter duplicates
# A mapping from letter to number
stoi = {s:i for i,s in enumerate(chars)}
stoi['<S>'] = 26
stoi['<E>'] = 27
# Copied from above, but now modified for mapping
for w in words:
chs = ['<S>'] + list(w) + ['<E>']
# Neat way for two char 'sliding-window'
for ch1, ch2 in zip(chs, chs[1:]):
ix1 = stoi[ch1]
ix2 = stoi[ch2]
N[ix1, ix2] += 1 # Increment cell in 2D by 1
可视化二元模型
如果我们将这个 N 数值化地可视化,它看起来会非常混乱。所以,让我们使用 matplotlib。
plt.imshow(N)
即使这样,看起来仍然有点难看。
让我们构建一些更美观的东西来可视化正在发生的事情。
itos = {i:s for s, i in stoi.items()} # Basically reversing stoi element order
plt.figure(figsize=(16, 16))
plt.imshow(N, cmap='Blues') # Heatmap basically
for i in range(28):
for j in range(28):
chstr = itos[i] + itos[j] # Add text for heat tiles
plt.text(j, i, chstr, ha="center", va="bottom", color="gray")
plt.text(j, i, N[i,j].item(), ha="center", va="top", color="gray")
plt.axis('off')
(-0.5, 27.5, 27.5, -0.5)
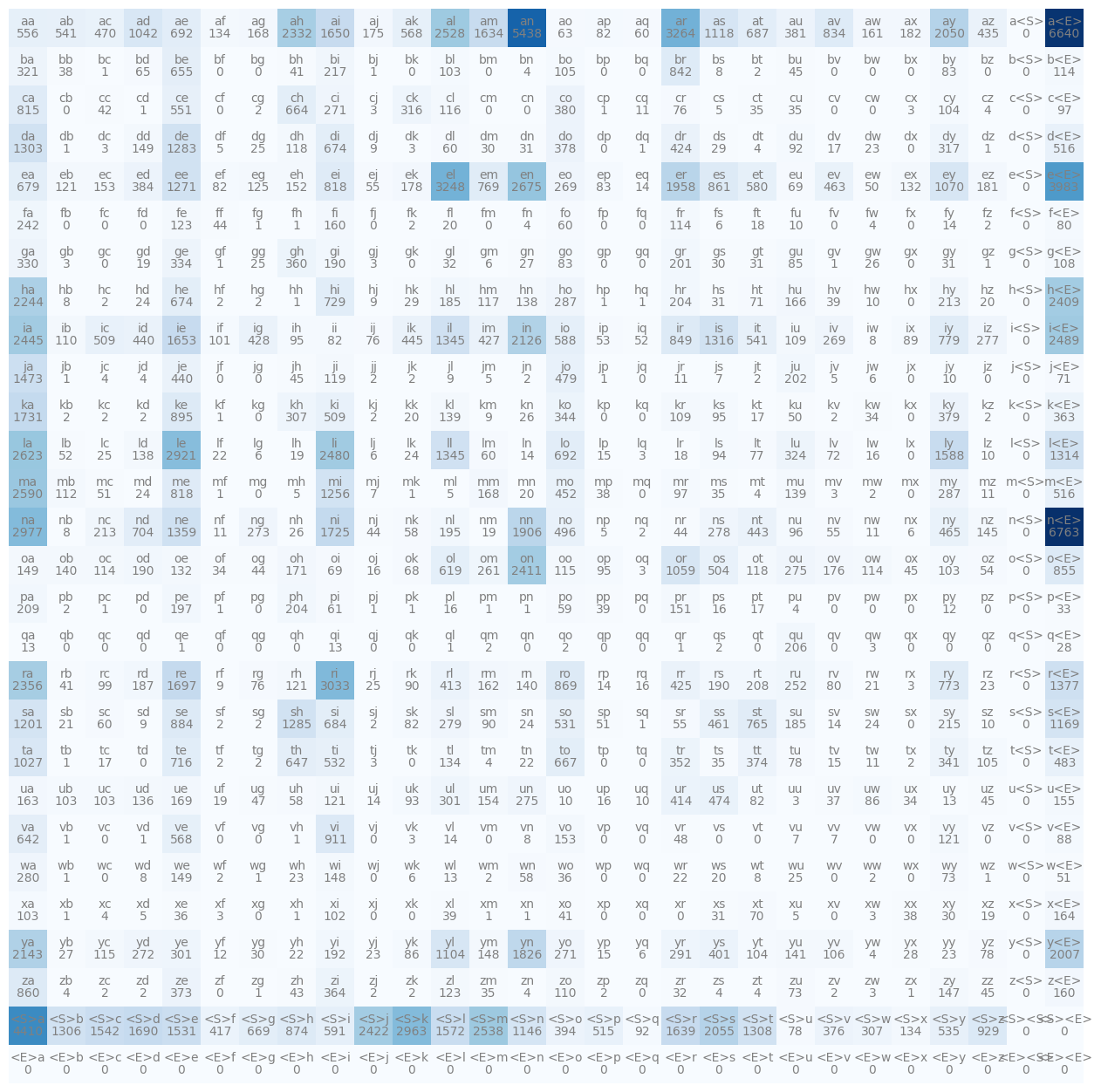
处理不可能的情况
如果你渲染这个模型,会发现有一行和一列会显示出 <S> 和 <E> 的问题。
对于像 (a, <S>)(倒数第二列)这样的实例有一个列,对于像 (<E>, a)(最后一行)这样的元组有一个行。
不可能的组合。
这个问题非常严重,以至于我们应该调整我们的模型。
这是通过将我们的特殊字符<S>和<E>替换为只有一个通用的特殊字符.来实现的。
N = torch.zeros((27, 27), dtype=torch.int32) # 28x28 -> 27x27
chars = sorted(list(set(''.join(words))))
stoi = {s:i+1 for i,s in enumerate(chars)}
stoi['.'] = 0 # Our special character now has position zero
itos = {i:s for s,i in stoi.items()}
# Copied from above, but now modified
for w in words:
chs = ['.'] + list(w) + ['.']
for ch1, ch2 in zip(chs, chs[1:]): # Neat way for two char 'sliding-window'
ix1 = stoi[ch1]
ix2 = stoi[ch2]
N[ix1, ix2] += 1 # Increment cell in 2D by 1
plt.figure(figsize=(16, 16))
plt.imshow(N, cmap='Blues') # Heatmap basically
for i in range(27):
for j in range(27):
chstr = itos[i] + itos[j] # Add text for heat tiles
plt.text(j, i, chstr, ha="center", va="bottom", color="gray")
plt.text(j, i, N[i,j].item(), ha="center", va="top", color="gray")
plt.axis('off')
(-0.5, 26.5, 26.5, -0.5)
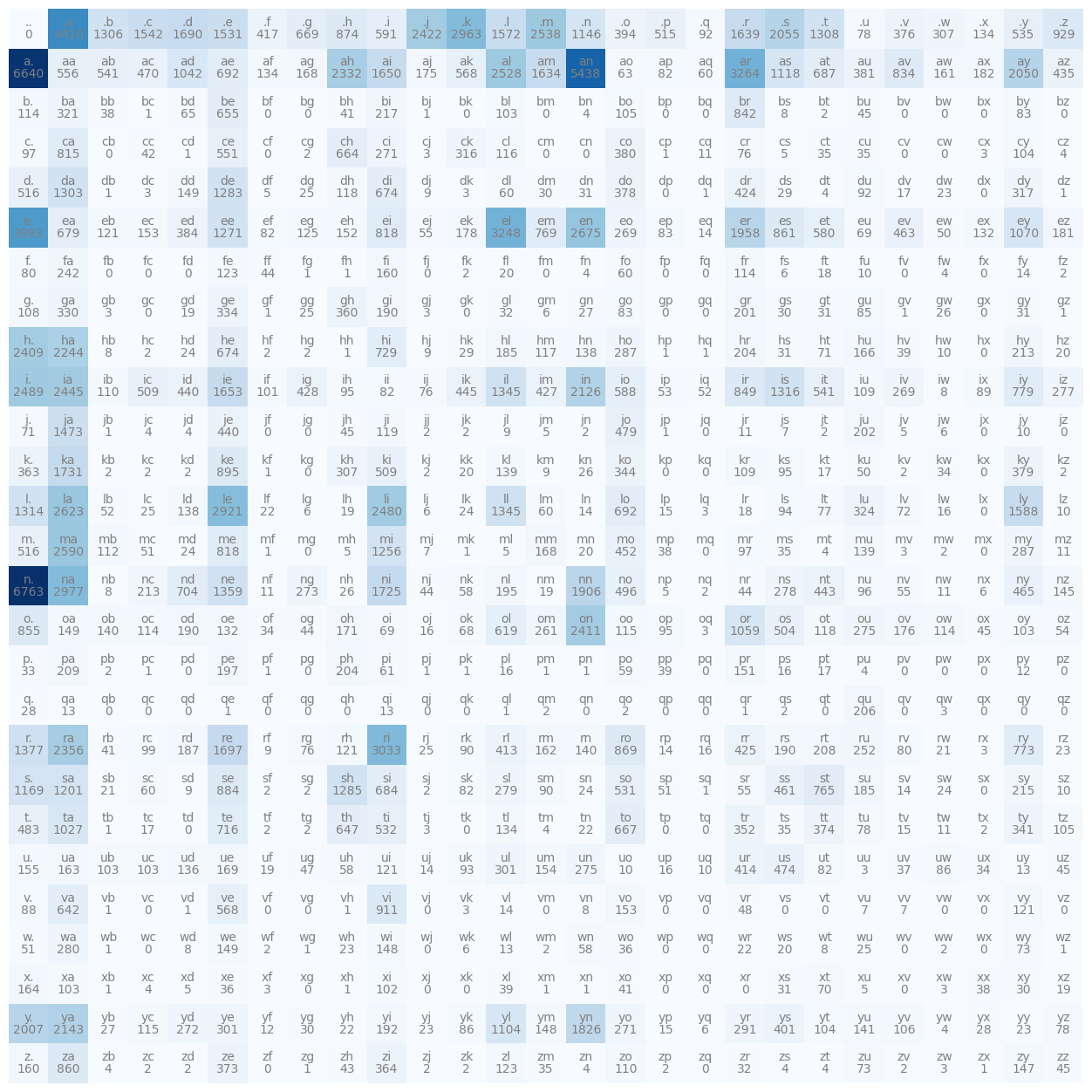
这样处理后,之前出现的冗余行-列问题就不存在了,因为 '.' 实际上现在确实可以出现在字母的前面或后面
(甚至从技术上讲,.. 也是合法的)。
构建概率分布
我们将遵循概率,并开始根据相关矩阵显示的行对模型进行逐行采样。
所以,我们从包含 ('.', 'a') 的行开始。
# Getting the entire zero-th row
# (a 1D array of '.' and all letters following)
print("Raw first row's combination counts:\n", N[0])
print(N[0].shape)
Raw first row's combination counts:
tensor([ 0, 4410, 1306, 1542, 1690, 1531, 417, 669, 874, 591, 2422, 2963,
1572, 2538, 1146, 394, 515, 92, 1639, 2055, 1308, 78, 376, 307,
134, 535, 929], dtype=torch.int32)
torch.Size([27])
由于我们想要进行采样,我们需要将原始计数按行转换为概率。
我们通过将每个单元格除以其所在行的单元格总和来实现这一点。这样,我们就得到了该行的概率分布。
p = N[0].float() # probability vector (np.array of floats)
p = p / p.sum() # normalized probability distribution
print("\nRow's distribution:\n", p)
Row's distribution:
tensor([0.0000, 0.1377, 0.0408, 0.0481, 0.0528, 0.0478, 0.0130, 0.0209, 0.0273,
0.0184, 0.0756, 0.0925, 0.0491, 0.0792, 0.0358, 0.0123, 0.0161, 0.0029,
0.0512, 0.0642, 0.0408, 0.0024, 0.0117, 0.0096, 0.0042, 0.0167, 0.0290])
让我们来探讨一下 p 的含义以及现在可以用它做些什么。
# Sampling from these distributions
# Torch.multinomial -> "Give me probability, I'll give you integer"
# We'll use a PyTorch Generator to make things repeatable (deterministic)
g = torch.Generator().manual_seed(2147483647)
p = torch.rand(3, generator=g) # Generate three random numbers [0;1]
p = p / p.sum() # compact these random numbers into a distribution
# output: [0.6064, 0.3033, 0.0903]
print(p)
tensor([0.6064, 0.3033, 0.0903])
从概率分布中采样
现在要从这个分布中采样,我们可以使用 torch.multinomial()。
这个函数接受一个概率分布,并根据给定的概率分布提供一定数量的整数样本。
# With probability distribution p, create a list of 20 samples
# [replacement: true] means drawing an element doesn't invalidate drawing this element again
torch.multinomial(p, num_samples=20, replacement=True, generator=g)
# We'd expect ~60% of the 20 items to be 0, ~30% to be 1 , ~10% to be 2
# output: [1, 1, 2, 0, 0, 2, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1]
tensor([1, 1, 2, 0, 0, 2, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1])
样本量越大,分布的近似/匹配就越精确。
我们现在使用相同的生成器,并将采样逻辑应用到我们的二维出现次数数组上。(或者说是它的第一行)
我们取每行的计数,将它们压缩成正态分布,并从中抽取一个样本。
p = N[0].float() # probability vector
p = p / p.sum() # normalized probability distributions
g = torch.Generator().manual_seed(2147483647)
ix = torch.multinomial(p, num_samples=1, replacement=True, generator=g).item()
# This is an index, a number representing a letter by probability
print(itos[ix]) # Convert index to letter
j
我们刚刚为第一个名字建议抽取了一个起始字符/标记 'j'。
有了这个,我们可以遍历数组,找到行名为 ('j', '.') 的行,并重复抽取过程。
从现在起,这是一个由概率驱动的循环。
g = torch.Generator().manual_seed(2147483647)
n = 20
for i in range(n):
ix = 0 # Start with special ('.', 'letter') token row
out = [] # hold the n names to be generated
while True:
p = N[ix].float() # probability vector
p = p / p.sum() # normalized probability distributions
# draw a single sample from this distribution, set this as new row index
ix = torch.multinomial(p, num_samples=1, replacement=True, generator=g).item()
out.append(itos[ix])
# if we find ourselves back in the special ('.', 'letter') row, we're done with this name
if ix == 0:
break
print(''.join(out))
junide.
janasah.
p.
cony.
a.
nn.
kohin.
tolian.
juee.
ksahnaauranilevias.
dedainrwieta.
ssonielylarte.
faveumerifontume.
phynslenaruani.
core.
yaenon.
ka.
jabdinerimikimaynin.
anaasn.
ssorionsush.
Et voilà,出现了像 junide 这样糟糕的名字建议。
尽管它的表现很糟糕,但它还算合理。尽管效率不高。让我们来改进这一点。
使用 p = N[ix].float() # 概率向量 时,我们总是在获取一行,并总是将这一行完全从整数转换为浮点数。
此外,每次迭代我们也会做 p = p / p.sum()。
最好是为此准备一个专门的、预处理过的矩阵 P;只是一个计算好的概率矩阵。
作为一步旁路,我们使用 P 来按行求和。这在之前是所有 27 个字母的 p.sum()。
让我们构建这个性能升级矩阵 P:
P = N.float()
# P /= P.sum() # This would sum over all elements, row- and column-wise -> wrong
# This is allowed with PyTorch:
P /= P.sum(1, keepdims=True) # sum: A 27x1 vector (1 stands for row-wise sum) (27 by 27 divided by 27 by 1 is possible in PyTorch -> broadcasting)
# For broadcasting to work like here, each dimension must be either equal or 1 (or not existent), which is the case here (dimensions will be aligned from right to left!)
# Keepdim=True means that the sum vector is 27x1, (the 1 before that stating that the no. of rows is to be kept, but columns are to be summed over per row)
g = torch.Generator().manual_seed(2147483647)
for i in range(20):
ix = 0
out = [] # Hold multiple names
while True:
p = P[ix]
# draw a single sample from this distribution
ix = torch.multinomial(p, num_samples=1, replacement=True, generator=g).item()
# If stopping special character is drawn
out.append(itos[ix])
if ix == 0:
break
print(''.join(out))
junide.
janasah.
p.
cony.
a.
nn.
kohin.
tolian.
juee.
ksahnaauranilevias.
dedainrwieta.
ssonielylarte.
faveumerifontume.
phynslenaruani.
core.
yaenon.
ka.
jabdinerimikimaynin.
anaasn.
ssorionsush.
# Quick sanity check for broadcasting
# Expected: Every row of P should sum up to 1
print(P.sum(1)) # 1 stands for row-wise sum
tensor([1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000,
1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000, 1.0000])
在这一点上,强烈建议阅读 PyTorch Broadcasting Semantics。真正理解它,不要只是粗略地看一遍。
广播可能会以你意想不到的方式接受事物并处理它们。
你真的需要理解你对广播的使用,以知道你在过程中是否犯了错误。
因为大多数时候,它不会告诉你。
生成名字的质量
我们通过计算字母组合的频率,然后进行归一化和基于该概率基础的采样,构建了一个二元语言模型。
我们训练了模型,我们从模型中进行了采样(逐字符迭代)。但它在想出名字方面仍然很差。
但到底有多差呢?我们知道模型的“知识”由 P 表示,但我们如何将模型的质量浓缩为一个值呢?
首先,让我们看看我们从数据集中创建的二元组:
例如,emma 的二元组是:.e, em, mm, ma, a.
模型为这些二元组分配了什么概率?
# Copied from above, but now modified
for w in words[:1]:
chs = ['.'] + list(w) + ['.']
for ch1, ch2 in zip(chs, chs[1:]): # Neat way for two char 'sliding-window'
ix1 = stoi[ch1]
ix2 = stoi[ch2]
prob = P[ix1, ix2]
print(f'{ch1}{ch2}: {prob:.4f}')
.e: 0.0478
em: 0.0377
mm: 0.0253
ma: 0.3899
a.: 0.1960
这会提供像 ma: 0.3899 这样的输出。
任何高于或低于 1/27 = 0.0370 的值意味着我们偏离了平均水平 / 我们从二元组统计中学到了一些东西。
我们再次通过计算数据集中每个二元组的出现次数,然后将计数归一化为概率来学习这一点。
好的,我们现在如何将这些概率总结为一个质量指标?
解决方案:对数似然,即所有单个标记概率的 \(\log(probability)\) 的总和(应用 \(log\) 是为了可读性,基本上是为了方便)
对数似然越高,模型越好,因为它更能从数据集中预测序列中的下一个字符。
log_likelihood = 0.0
n = 0 # tuple count
# copied from above, but now modified - Log likelihood over all words
for w in words:
chs = ['.'] + list(w) + ['.']
for ch1, ch2 in zip(chs, chs[1:]): # Neat way for two char 'sliding-window'
ix1 = stoi[ch1]
ix2 = stoi[ch2]
prob = P[ix1, ix2]
logprob = torch.log(prob)
log_likelihood += logprob
n += 1
# print(f'{ch1}{ch2}: {prob:.4f} {logprob:.4f}')
print(f'{log_likelihood=}') # As this is a tensor and we want to see that too
nll = -log_likelihood
print(f'{nll=}') # Negative log likelihood
print(f'{nll/n}') # Average negative log likelihood (this is the loss we want to minimize)
log_likelihood=tensor(-559891.7500)
nll=tensor(559891.7500)
2.454094171524048
我们计算了负对数似然,因为这是遵循将目标设定为最小化损失函数的惯例。损失/负对数似然越低,模型越好。
概率越小,对数似然就越负。这就是为什么它被反转到正空间。负对数似然
nll越高,模型越差。
通常这个nll也会被归一化,得到平均(负)对数似然。
我们的模型得到了 2.45。越低越好。
我们需要找到减少这个值的参数。
目标:
最大化训练数据相对于模型参数 P 的似然度
等同于:最大化对数似然(因为 \(log\) 是单调的)
等同于:最小化负对数似然
等同于:最小化平均负对数似然(如上所示的 2.45,作为质量度量)
从现在开始,我们模型的问题可以通过查看我们的损失函数,即负对数似然来可视化。
下面立即出现了一个问题:
log_likelihood = 0.0
n = 0
# Copied from above, but now modified
for w in ['andrejq']:
chs = ['.'] + list(w) + ['.']
for ch1, ch2 in zip(chs, chs[1:]): # Neat way for two char 'sliding-window'
ix1 = stoi[ch1]
ix2 = stoi[ch2]
prob = P[ix1, ix2]
logprob = torch.log(prob)
log_likelihood += logprob
n += 1
print(f'{ch1}{ch2}: {prob:.4f} {logprob:.4f}')
print(f'\n{log_likelihood=}') # As this is a tensor and we want to see that too
nll = -log_likelihood
print(f'{nll=}')
print(f'{nll/n}')
.a: 0.1377 -1.9829
an: 0.1605 -1.8296
nd: 0.0384 -3.2594
dr: 0.0771 -2.5620
re: 0.1336 -2.0127
ej: 0.0027 -5.9171
jq: 0.0000 -inf
q.: 0.1029 -2.2736
log_likelihood=tensor(-inf)
nll=tensor(inf)
inf
使用名字 andrejq 我们得到了平均负对数似然为 \(\infty\)。这是一个无限大的损失,即模型性能的“最坏情况”。
这是因为二元组 jq 从未在我们的训练数据中出现过,它的计数就是 0,因此概率是 \(0\%\)。
因此,模型选择这个二元组的概率是 \(log(0) = -\infty\),极大地扭曲了负对数似然。
这确实有点糟糕。
模型平滑
模型平滑相对容易解决这个问题。
我们基本上将我们拥有的每个计数增加 1,以避免计数为 0:
P = (N+1).float() # Adding a lot more means smoothing out distributions more; see NN approach for discussing this
# This is allowed with PyTorch:
P /= P.sum(1, keepdims=True) # sum: A 27x1 vector (1 stands for row-wise sum)
我们在 N 上加上 +1,这样我们就避免了由 \(log\) 引起的 \(\infty\)。
在平滑处理后,重新运行与之前相同的代码,现在给二元组 jq 赋予了一个(非常小的)概率。
模型对这组二元组感到惊讶,但不再被压倒。
log_likelihood = 0.0
n = 0
# Copied from above, but now modified
for w in ['andrejq']:
chs = ['.'] + list(w) + ['.']
for ch1, ch2 in zip(chs, chs[1:]): # Neat way for two char 'sliding-window'
ix1 = stoi[ch1]
ix2 = stoi[ch2]
prob = P[ix1, ix2]
logprob = torch.log(prob)
log_likelihood += logprob
n += 1
print(f'{log_likelihood=}') # As this is a tensor and we want to see that too
nll = -log_likelihood
print(f'{nll=}')
print(f'{nll/n}')
log_likelihood=tensor(-27.8672)
nll=tensor(27.8672)
3.4834020137786865
到目前为止,这是一个相当可靠的二元字符估计模型。我们已经评估了性能,并通过平滑处理消除了漏洞。但它仍然有些不稳定。
神经网络方法 - 相同的问题,不同的解决方案
现在,我们将字符估计问题纳入神经网络的框架中。
我们处理的问题仍然相同,方法变化了,结果应该看起来相似。
我们的神经网络接收一个单个字符并输出下一个可能字符的概率分布(在这种情况下是 \(27\) 个)。
它将对最有可能跟随的字符进行猜测。
这仍然可以通过相同的损失函数来衡量性能,即负对数似然。
由于我们有训练数据,我们知道每个训练示例中实际跟随的字符。
这可以用于调整神经网络,使其做出更好的猜测。监督学习在行动。
#Create training set of all bigrams
xs, ys = [], [] # Input and output character indices
for w in words:
chs = ['.'] + list(w) + ['.']
for ch1, ch2 in zip(chs, chs[1:]):
ix1 = stoi[ch1]
ix2 = stoi[ch2]
xs.append(ix1)
ys.append(ix2)
# Convert lists to tensors
xs = torch.tensor(xs)
ys = torch.tensor(ys)
对于名字 .emma.,xs(输入)和 ys(输出)会看起来像这样:
#Create training set of one particular bigram
xs, ys = [], []
for w in words[:1]:
chs = ['.'] + list(w) + ['.']
for ch1, ch2 in zip(chs, chs[1:]):
ix1 = stoi[ch1]
ix2 = stoi[ch2]
print(f'{ch1}{ch2}: {ix1} -> {ix2}')
xs.append(ix1)
ys.append(ix2)
xs = torch.tensor(xs)
ys = torch.tensor(ys)
print(xs)
print(ys)
.e: 0 -> 5
em: 5 -> 13
mm: 13 -> 13
ma: 13 -> 1
a.: 1 -> 0
tensor([ 0, 5, 13, 13, 1])
tensor([ 5, 13, 13, 1, 0])
在 PyTorch 中,torch.tensor 是一个函数,用于构造并返回一个 torch.Tensor 实例。而 torch.Tensor 本身是所有 PyTorch 张量的类。通常情况下,除非需要初始化一个完全空的张量,否则没有理由优先选择 torch.Tensor 而不是 torch.tensor。值得注意的是,torch.Tensor 是 torch.FloatTensor 的别名,因此默认的数据类型(dtype)是 torch.float32。
强烈建议使用 torch.tensor。
向网络输入数据
将字母的数字表示作为单个输入神经元的输入是没有意义的。网络将引用数值本身,而不会考虑可能的上下文,如可能的值范围等。尽管与数字相关的字母由于与其他字母的关系而在其索引位置,但这并不会被表达出来。
独热编码(One-Hot Encoding) 在这种情况下会好得多。
使用独热编码,我们取字母的整数值,例如 13,并创建一个全为 0 的向量,除了在第 13 个位置放置一个 1。
xenc = F.one_hot(xs, num_classes=27).float() # num_classes removes the need for F's guessing
xenc.shape # For '.emma' this will be [5, 27]
plt.imshow(xenc) # '. e m m a' (remember, this is the input, output would be 'e m m a .' for this example)
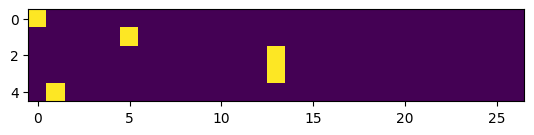
将单词的字符映射到整数,再映射到 float32 类型的向量。
这意味着它们可以作为神经网络(NNs)的输入。
让我们用神经元进行实验。我们构建一个 \(27\) 维的神经元,并用我们名字 .emma(共 \(5\) 个字母)逐字母输入来处理它。
W = torch.randn((27,1), generator=g) # the neuron: random column vector of 27 numbers from normal distribution
a = xenc @ W # '@' is PyTorch's matrix multiplication operator (5x27 @ 27x1 -> 5x1)
print(a) # this is now a 5x1 vector
tensor([[ 0.1066],
[-1.2464],
[-0.6378],
[-0.6378],
[ 1.8598]])
W 是一个 单个 神经元。
将它与 xenc 相乘使其对独热编码的输入产生“反应”。结果是 \(5\times 1\) 的向量。
.emma 有 5 个字符,我们有 1 个神经元。
该向量显示了每个字符的神经元激活情况;可以说是它对字符的反应。
由于输入是独热编码的,单个神经元接收一个“宽度为 27 的字符”。
在这个例子中,它同时对所有 5 个字母这样做。对于每个 27 维的字母,它输出一个激活值。它没有从中学习,但这是基本思想。
关键的洞察是,由于一个字母通过独热编码有 27 个维度,单个神经元也必须有 27 个维度。
现在,这只是 一个 神经元。我们想要 27 个神经元。“每个可能的字符一个神经元”的原因稍后会变得显而易见。
W = torch.randn((27,27), generator=g) # random column matrix of 27x27 numbers (previous was 27x1 for a single neuron)
a = xenc @ W # @ is PyTorch's matrix multiplication operator, this is now a 5x27 vector
print(a) # this is now a 5x27 vector
tensor([[ 0.2603, 0.9090, -1.4458, 1.1072, -0.7175, -0.3867, -1.2542, 1.2068,
-0.7305, -1.0926, 0.3223, 0.0717, -0.2774, 1.1634, -0.6691, 0.6492,
-0.8157, 0.6404, 1.0442, -1.1571, 0.5107, 0.7593, -1.6086, -0.1607,
-0.7226, 0.5205, 0.7270],
[ 0.9641, 0.0471, 0.3096, 1.2087, -0.9954, -0.4485, -1.2345, 1.1220,
-0.6738, 0.6365, -0.5964, 1.3058, 0.3857, -0.7510, 0.9278, -1.4849,
-0.2129, -0.9419, 1.5729, 1.0105, -0.1085, 0.6006, -0.7091, 1.9217,
-0.1818, -0.0954, -0.9253],
[-0.4645, -0.5206, -0.5579, 1.1087, 0.4149, 0.9557, -0.1471, -1.2532,
-1.1850, 2.1940, 0.6698, 0.4829, 2.0022, -0.6284, -0.9379, 1.6772,
0.0039, -0.1460, -1.2915, -0.0748, 1.3272, 1.6676, 1.3931, 0.6540,
-0.2245, -1.8563, 0.9609],
[-0.4645, -0.5206, -0.5579, 1.1087, 0.4149, 0.9557, -0.1471, -1.2532,
-1.1850, 2.1940, 0.6698, 0.4829, 2.0022, -0.6284, -0.9379, 1.6772,
0.0039, -0.1460, -1.2915, -0.0748, 1.3272, 1.6676, 1.3931, 0.6540,
-0.2245, -1.8563, 0.9609],
[ 0.1114, -0.5977, -0.3977, -1.2801, 0.0924, -0.1463, -0.5254, -1.5195,
0.3240, -1.5065, 1.2898, -1.5100, 1.0930, 0.0549, 1.3537, -1.0896,
0.2558, 0.2469, 0.3190, -0.9861, -0.2138, -3.0010, 1.4111, 0.0317,
-0.5475, 0.8183, -0.8163]])
这将并行评估所有 27 个神经元对所有 5 个示例的处理。输出现在是一个 \(5\times 27\) 的矩阵。
这意味着: 对于每一个 27 个神经元,我们得到了该神经元在每一个 5 个示例上的激活率。
(xenc @ W)[3, 13] # The firing rate of the 14th neuron at the 4th input
tensor(-0.6284)
现在我们已经将 5 个 27 维的输入喂入了 27 个神经元的输入层。 我们不会添加偏置或任何其他东西。这就是网络结构方面的全部内容。
恢复正态分布
直观地说,我们希望每个输入(每个字符)的神经元能够产生一个 27 维的激活值,这些值可以被转换成下一个要选取的字符的正态分布。我们已经通过二元模型的概率分布看到了这一点,它为每个字符提供了关于最可能跟随的字符的信息。
问题: 目前我们还没有这样的分布。 对于每个字符,我们得到了 27 个数字。正数、负数,应有尽有。 而正态分布并不是直接从神经网络中产生的。 神经网络并不是这样工作的。
解决方案: 对于每个字符,我们并不期望像上面在 可视化二元模型 中展示的矩阵可视化那样得到可能组合的计数, 而是“对数计数”。 基于这种解释,我们对它们进行指数化处理。
logits = xenc @ W # logits, different word for log-counts
# These two combined are called Softmax -> Build a probability distribution from logits
counts = logits.exp() # negative numbers are positive below 1, positive numbers are positive above 1
# Let's just say the counts variable holds something like 'fake counts', kinda like in the N matrix of bigram, we process them just the same
probs = counts / counts.sum(1, keepdims=True) # Normal distribution probabilities
print(probs.shape) # 5x27, as expected
print(probs[0].sum()) # Will be 1. for any index [0-4]
torch.Size([5, 27])
tensor(1.)
这听起来可能有些奇怪,坦白说,看起来也有点奇怪,但现在我们有一组数字,我们可以像在二元组方法中处理实际计数那样对待它们。
没有负数存在。(“假装它是一个类似计数的东西”)。
这样,我们的任务就变成了寻找合适的权重 W,以便让网络输出正确的字符索引。
回顾
给定示例输入 .emma.,神经网络一次处理每个字符。
我们从输入 x = . 和标签 y = e 开始,依此类推。
- 我们获取
.的索引,它是0 - 我们根据索引
0将.独热编码,形成一个 27 维向量 - 这个向量以 \(27 \times 1\) 向量的形式输入到神经网络中
- 在网络中,它激活了 27 个不同的 27 维神经元
- 因此,对于
.的激活形成了一个 \(1 \times 27\) 矩阵 - 然后应用 Softmax:
- 将激活值/对数几率通过 \(e^x\) 转换,使它们进入 \((0;\infty)\) 范围
- 通过计算它们的组合归一化概率,再次替换这 27 个偏移的对数几率值
(将 Softmax 视为一种归一化函数,它接收奇怪的数字,返回一个正态分布。这些归一化概率必须指示哪个字母必须跟随例如输入 .)
现在的问题是:
我们能找到一组权重 W,使得网络设置的概率是好的吗?
上述/下述操作是可微分的,因此可以反向传播。 为了完整性,这里再次列出它们:
# FORWARD-PASS:
xenc = F.one_hot(xs, num_classes=27).float() # one-hot encode the names
logits = xenc @ W # logits, different word for log-counts
# Softmax as part of forward pass
counts = logits.exp() # 'fake counts', kinda like in the N matrix of bigram
probs = counts / counts.sum(1, keepdims=True) # Normal distribution probabilities
print(probs.shape)
torch.Size([5, 27])
目前,神经网络能够做到以下几点:
nlls = torch.zeros(len(xs)) # 5
# Five bigrams making up '.emma.'
for i in range(len(xs)):
#i-th bigram
x = xs[i].item() # input character-index
y = ys[i].item() # output character-index
print("\n-------\n")
print(f'bigram example tuple {i+1}: ("{itos[x]}", "{itos[y]}") (indexes ({x}, {y}))') # Input is index x, expected output is index y
print('\t>> input to the neural net:', x, f'({itos[x]})') # Again, x, the index, is the NN's input
print('\t>> output probabilities from the neural net:', probs[i]) # We built probs in the above cell
print('\t>> most likely next character:', itos[probs[i].argmax().item()], f'(index {probs[i].argmax().item()}, likelihood {probs[i].max().item()})') # argmax() returns the index of the highest value in probs[i]
print('\t>> label (actual next character):', y)
p = probs[i, y]
print('\t>> probability assigned by the net to the correct character:', p.item())
logp = torch.log(p)
print('\t>> log likelihood:', logp.item())
nll = -logp
print('\t>> negative log likelihood:', nll.item())
nlls[i] = nll
print('\n============\n')
print('average negative log likelihood, i.e. loss =', nlls.mean().item())
-------
bigram example tuple 1: (".", "e") (indexes (0, 5))
>> input to the neural net: 0 (.)
>> output probabilities from the neural net: tensor([0.0360, 0.0688, 0.0065, 0.0839, 0.0135, 0.0188, 0.0079, 0.0926, 0.0134,
0.0093, 0.0383, 0.0298, 0.0210, 0.0887, 0.0142, 0.0530, 0.0123, 0.0526,
0.0787, 0.0087, 0.0462, 0.0592, 0.0055, 0.0236, 0.0135, 0.0466, 0.0573])
>> most likely next character: g (index 7, likelihood 0.09264726936817169)
>> label (actual next character): 5
>> probability assigned by the net to the correct character: 0.018827954307198524
>> log likelihood: -3.972412586212158
>> negative log likelihood: 3.972412586212158
-------
bigram example tuple 2: ("e", "m") (indexes (5, 13))
>> input to the neural net: 5 (e)
>> output probabilities from the neural net: tensor([0.0582, 0.0233, 0.0303, 0.0744, 0.0082, 0.0142, 0.0065, 0.0682, 0.0113,
0.0420, 0.0122, 0.0819, 0.0327, 0.0105, 0.0561, 0.0050, 0.0179, 0.0087,
0.1070, 0.0610, 0.0199, 0.0405, 0.0109, 0.1517, 0.0185, 0.0202, 0.0088])
>> most likely next character: w (index 23, likelihood 0.15169577300548553)
>> label (actual next character): 13
>> probability assigned by the net to the correct character: 0.010476764291524887
>> log likelihood: -4.558595657348633
...
============
average negative log likelihood, i.e. loss = 4.237281322479248
Output is truncated. View as a scrollable element or open in a text editor. Adjust cell output settings...
损失确实不理想,我们可以通过重新采样网络权重来尝试改善结果。或许我们能得到更好的结果?可能会,但我们不应该依赖于偶然性。
让我们系统地进行优化。
优化
偶然地,为权重初始化的生成器种子加上 1 可能会产生更小的整体损失。但是,等待随机性带来最优解是业余的做法。
计算损失相对于矩阵
W(每个示例)的梯度,我们可以将W调整到优化的方向。这就是基于梯度的优化。
对于示例 .emma.,这意味着必须分别调整这些特定的神经元激活部分:
# Activations of the respective character input
print('intput ".", output "e":', probs[0, 5]) # input: ., probability shown for: e to be drawn
print('intput "e", output "m":', probs[1, 13])
print('intput "m", output "m":', probs[2, 13])
print('intput "m", output "a":', probs[3, 1])
print('intput "a", output ".":', probs[4, 0])
intput ".", output "e": tensor(0.0188)
intput "e", output "m": tensor(0.0105)
intput "m", output "m": tensor(0.0092)
intput "m", output "a": tensor(0.0102)
intput "a", output ".": tensor(0.0342)
由于我们希望根据给定的输入改变这些特定值,我们需要能够访问它们。
结果表明,我们可以使用 PyTorch 非常方便地做到这一点。
# Over the length of probs (dimension 0), we plug out per row (a row is 27 wide) the corresponding index stated in ys at the same index
probs[torch.arange(len(probs)), ys] # The probabilities the NN assigns to the correct next character
tensor([0.0188, 0.0105, 0.0092, 0.0102, 0.0342])
现在,正如上面提到的,我们想要从这些值中看到负的平均对数似然。
loss = -probs[torch.arange(len(probs)), ys].log().mean()
print(loss.item()) # just like above
4.237281322479248
由于我们需要在每次迭代/每个字母输入神经网络时计算这个损失,我们现在**将这个损失添加到前向传播流程中。**这使得反向传播有机会“看到”网络的“不准确之处”并据此采取行动。
g = torch.Generator().manual_seed(2147483647)
W = torch.randn((27,27), device=torch.device("cpu"), generator=g, requires_grad=True) # random column matrix of 27x27 numbers (requires_grad=True for autograd)
# FORWARD-PASS:
xenc = F.one_hot(xs, num_classes=27).float() # one-hot encode the names
logits = xenc @ W # logits, different word for log-counts
# Softmax:
counts = logits.exp() # 'fake counts', kinda like in the N matrix of bigram
probs = counts / counts.sum(1, keepdims=True) # Normal distribution probabilities (this is y_pred)
loss = -probs[torch.arange(len(probs)), ys].log().mean()
print('Loss:',loss.item())
Loss: 3.7693049907684326
反向传播
W.grad = None # Make sure all gradients are reset to zero
loss.backward() # Torch kept track of what this variable is, kinda cool
# Looking at Backward-Pass' impact
W.grad # There's now stuff inside here
print(W.shape) # 27x27 gradients for the neurons
print(W.grad[0,0]) # First neuron's value for letter probability of '.' should be raised by this to cause more loss
torch.Size([27, 27])
tensor(0.0121)
因为我们在 W 上设置了 requires_grad=True,PyTorch 将会跟踪对 W 执行的操作,并能够计算损失相对于 W 的梯度,就像我们在 Micrograd 中手动完成的那样。梯度告诉我们为了更有效地最大化损失需要做什么。但反过来,我们可以使用这些值来更新神经元权重。
让我们这样做:
W.data += -0.1 * W.grad # Update weights with gradient descent by 0.1 as learning rate
遍历最后三个代码单元是梯度下降。我们有效地减少了每次迭代神经网络的损失。
总结
让我们将到目前为止所学和应用的内容压缩成三个代码块,并将它们应用到整个训练集上:
# Create training set of one particular bigram
xs, ys = [], []
for w in words:
chs = ['.'] + list(w) + ['.']
for ch1, ch2 in zip(chs, chs[1:]):
ix1 = stoi[ch1]
ix2 = stoi[ch2]
xs.append(ix1)
ys.append(ix2)
xs = torch.tensor(xs)
ys = torch.tensor(ys)
num = xs.nelement()
print('number of examples', num)
number of examples 228146
# Initialize the network
g = torch.Generator(device=device).manual_seed(2147483647)
W = torch.randn((27,27), device=device, generator=g, requires_grad=True) # random column matrix of 27x27 numbers (requires_grad=True for autograd)
# Training cycles, using the entire dataset -> 200 Epochs
for k in range(200):
# Forward pass
xenc = F.one_hot(xs, num_classes=27).float().to(device) # one-hot encode the names
logits = xenc @ W # logits, different word for log-counts
counts = logits.exp() # 'fake counts', kinda like in the N matrix of bigram
probs = counts / counts.sum(1, keepdims=True) # Normal distribution probabilities (this is y_pred)
loss = -probs[torch.arange(len(probs)), ys].log().mean()
print(f'Loss @ iteration {k+1}: {loss}')
# Backward pass
W.grad = None # Make sure all gradients are reset
loss.backward() # Torch kept track of what this variable is, kinda cool
# Weight update
W.data += -50 * W.grad
Loss @ iteration 1: 3.7109203338623047
Loss @ iteration 2: 3.3591017723083496
Loss @ iteration 3: 3.136110305786133
Loss @ iteration 4: 2.996102809906006
Loss @ iteration 5: 2.901326894760132
Loss @ iteration 6: 2.832087278366089
Loss @ iteration 7: 2.780813217163086
Loss @ iteration 8: 2.7420215606689453
Loss @ iteration 9: 2.7117466926574707
Loss @ iteration 10: 2.6873340606689453
Loss @ iteration 11: 2.6671009063720703
Loss @ iteration 12: 2.6499812602996826
Loss @ iteration 13: 2.635272264480591
Loss @ iteration 14: 2.622483253479004
Loss @ iteration 15: 2.6112561225891113
Loss @ iteration 16: 2.6013193130493164
Loss @ iteration 17: 2.5924623012542725
Loss @ iteration 18: 2.584519386291504
Loss @ iteration 19: 2.5773584842681885
Loss @ iteration 20: 2.5708725452423096
Loss @ iteration 21: 2.564974546432495
Loss @ iteration 22: 2.5595920085906982
Loss @ iteration 23: 2.554664134979248
Loss @ iteration 24: 2.550138235092163
Loss @ iteration 25: 2.5459702014923096
...
Loss @ iteration 197: 2.462291717529297
Loss @ iteration 198: 2.4622433185577393
Loss @ iteration 199: 2.46219539642334
Loss @ iteration 200: 2.4621477127075195
Output is truncated. View as a scrollable element or open in a text editor. Adjust cell output settings...
上述明确的二元组计数概率分布方法与这个训练过的神经网络的精确度大致相同。
它的损失是 2.4540,我们现在的神经网络是 2.46。
这是因为我们基本上在做同样的事情,模仿我们之前在二元组模型中拥有的从计数到分布的关系。
但是, 这种神经网络方法要灵活得多。我们可以复杂化神经网络或进一步训练它。
确保你理解这个基本方法:
- 拥有权重,
- 计算它们的激活,
- 将它们转化为概率,以及
- 根据从 ys 和这些概率计算出的损失来优化权重,不会改变太多。
随着我们继续,它只会成为一个更有层次的系统。唯一有所变化的是激活计算,因为现在这将是分层的。
我们如何利用神经网络的灵活性来扩展二元组方法并不那么明显。然而,它确实是可能的。
考虑扩展神经网络,使其能够测量不仅仅是 (a, b) 类型的二元组,也许是 (a, b, ..., c) 的概率。
如果你有最后 10 个字符需要评估,你就不应该继续保持二元组风格的表格方法。
二元组方法扩展性不好,而神经网络的优势正是这一点。
与二元组方法一样,神经网络方法也有一个相当于平滑的等价物。
当权重 W 不是随机初始化的,比如说,它们全部都是 0,这将只会导致一个均匀分布的 probs。
你在损失函数中越鼓励
W接近零,分布就越平滑,它就变得越均匀。
这引导我们到了一个叫做正则化的概念。这通过一个小项,一个正则化损失,来增加/扩展损失函数。例如,我们可以平均 W 的平方项。这个值被视为额外的成本。 如果 W 只由零组成,即一个最优的均匀分布,它的值将为零。它对成本的影响由一个额外的因素 \(\lambda\) 控制。
将这想象为一种引力,轻轻地将 W 推向全为零的状态。这种推动也作用于分布,使它们更加均匀,更统一。
print("Additional term to be appended to the loss function, morphing it to regularize W:")
(W**2).mean().item()
Additional term to be appended to the loss function, morphing it to regularize W:
2.146524429321289
# Training cycles, using the entire dataset -> 200 Epochs
for k in range(200):
# Forward pass
xenc = F.one_hot(xs, num_classes=27).float().to(device) # one-hot encode the names
logits = xenc @ W # logits, different word for log-counts
counts = logits.exp() # 'fake counts', kinda like in the N matrix of bigram
probs = counts / counts.sum(1, keepdims=True) # Normal distribution probabilities (this is y_pred)
loss = -probs[torch.arange(len(probs)), ys].log().mean() + 0.01 * (W**2).mean()
print(f'Loss @ iteration {k+1}: {loss}')
# Backward pass
W.grad = None # Make sure all gradients are reset
loss.backward() # Torch kept track of what this variable is, kinda cool
# Weight update
W.data += -50 * W.grad
Loss @ iteration 1: 2.4835662841796875
Loss @ iteration 2: 2.4835257530212402
Loss @ iteration 3: 2.483488082885742
Loss @ iteration 4: 2.483452796936035
Loss @ iteration 5: 2.483419179916382
Loss @ iteration 6: 2.483386516571045
Loss @ iteration 7: 2.4833555221557617
Loss @ iteration 8: 2.4833250045776367
Loss @ iteration 9: 2.4832959175109863
Loss @ iteration 10: 2.4832677841186523
Loss @ iteration 11: 2.4832401275634766
Loss @ iteration 12: 2.4832139015197754
Loss @ iteration 13: 2.483187437057495
Loss @ iteration 14: 2.4831619262695312
Loss @ iteration 15: 2.483137607574463
Loss @ iteration 16: 2.4831132888793945
Loss @ iteration 17: 2.4830894470214844
Loss @ iteration 18: 2.4830663204193115
Loss @ iteration 19: 2.483043909072876
Loss @ iteration 20: 2.4830214977264404
Loss @ iteration 21: 2.482999801635742
Loss @ iteration 22: 2.482978343963623
Loss @ iteration 23: 2.482957601547241
Loss @ iteration 24: 2.4829370975494385
Loss @ iteration 25: 2.482917070388794
...
Loss @ iteration 197: 2.481318712234497
Loss @ iteration 198: 2.481313943862915
Loss @ iteration 199: 2.481309652328491
Loss @ iteration 200: 2.4813051223754883
Output is truncated. View as a scrollable element or open in a text editor. Adjust cell output settings...
# Finally, sample from this neural network model
# (This structure is copied from the bigram approach)
g = torch.Generator(device=device).manual_seed(2147483642)
for i in range(5):
out = []
ix = 0
while True:
# ----------
# BEFORE:
#p = P[ix] # Bigram explicit probability approach
# ----------
# NOW:
xenc = F.one_hot(torch.tensor([ix]), num_classes=27).float().to(device)
logits = xenc @ W # predict log-counts
counts = logits.exp() # counts, equivalent to N
p = counts / counts.sum(1, keepdims=True) # probabilities for next character
# ----------
ix = torch.multinomial(p, num_samples=1, replacement=True, generator=g).item()
out.append(itos[ix])
if ix == 0:
break
print(''.join(out))
kana.
jallet.
aye.
jalia.
zia.
这个模型基本上与二元组模型相同,但实现方式完全不同,导致结果相同但模型属性不同。神经网络要灵活得多。
在接下来的部分中,神经网络将扩展/复杂化,一直到变换器。