从一个直观问题开始

在处理音频、语音或其他时间序列数据时，我们几乎一定会遇到这样一个问题：如果两段信号在“内容”上是相似的，但在时间推进的速度上并不一致，我们还能不能判断它们是相似的吗？

这个问题在真实场景中非常常见。例如，两个人唱的是同一段旋律，但一个人唱得偏快、另一个人唱得偏慢；学生在视唱时可能会因为犹豫而放慢速度，唱错后回拉重唱，或者在某些位置突然加速；同一句话，被不同的人用不同的语速、不同的停顿方式说出来。
在这些情况下，如果我们强行要求“第 1 帧对第 1 帧，第 2 帧对第 2 帧”，那么几乎所有真实样本都会被简单粗暴地判定为“不相似”。

DTW（Dynamic Time Warping，动态时间规整） 正是为了解决这一类“时间轴对不上，但内容本质相似”的问题而提出的。它关注的并不是时间点是否严格一致，而是：在允许时间发生伸缩的前提下，两段序列能不能以一种合理的方式对应起来。

DTW 的核心思想：允许时间被拉伸

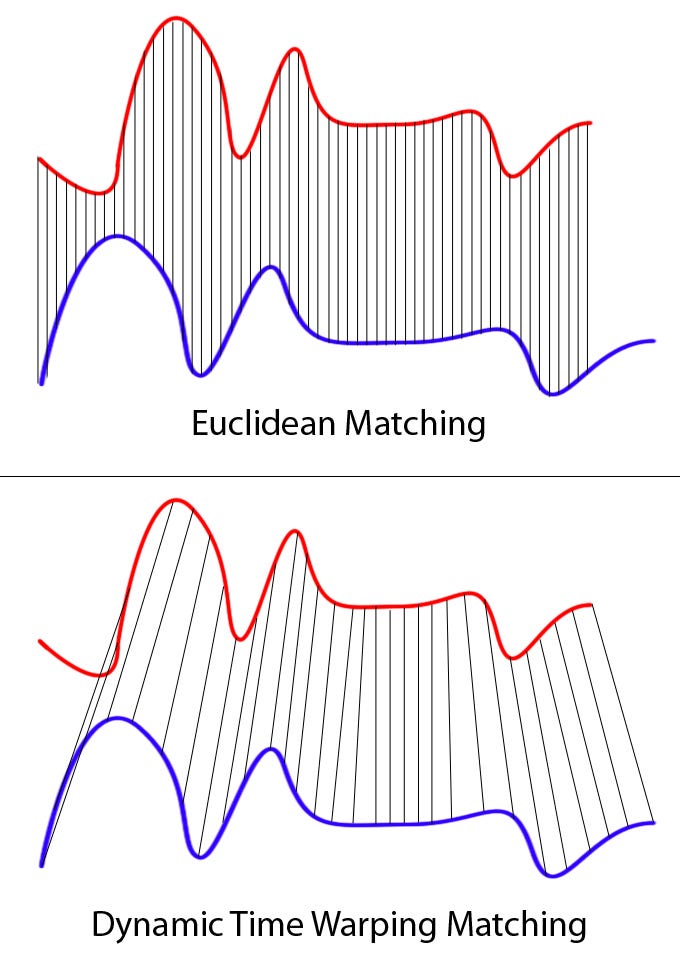
从直觉上看，DTW 的思想并不复杂。它并不要求两段序列在时间上同步前进，而是允许一段序列在某些地方“走快一点”，在另一些地方“走慢一点”，只要整体趋势和形状尽可能一致即可。换句话说，DTW 关注的是“形状是否相似”，而不是“时间是否对齐”。

在数学上，我们通常将两段时间序列表示为：

\[ X = (x_1, x_2, \dots, x_N), \quad Y = (y_1, y_2, \dots, y_M) \]

这里的 \(x_i\) 和 \(y_j\) 并不是原始音频采样点，而是在第 \(i\)、第 \(j\) 个时间位置提取到的特征帧。需要注意的是，序列长度 \(N\) 和 \(M\) 并不要求相等，这本身就已经体现了“时间不必同步”的思想。

接下来，DTW 会构造一个大小为 \(N \times M\) 的距离矩阵：

\[ D(i, j) = \lVert x_i - y_j \rVert \]

你可以把这个矩阵理解为一个全面的对照表：它回答的问题是，“序列 X 在第 \(i\) 个时刻的状态，与序列 Y 在第 \(j\) 个时刻的状态，到底有多不像？”
矩阵中的每一个格子，都是一次潜在的“对齐选择”。

在距离矩阵中“走一条路”

DTW 并不是在距离矩阵中简单地找一个最小值，而是要在整个矩阵中寻找一条从左上角走到右下角的路径。左上角 \((1,1)\) 表示两个序列的起点，右下角 \((N,M)\) 表示两个序列的终点，而路径上经过的每一个格子，都代表了一次“第 \(i\) 帧对齐到第 \(j\) 帧”的决策。

这条路径并不是随意的，它必须满足三个非常直观的约束。首先是单调性：时间只能向前推进，不能回到过去；其次是连续性：路径的每一步只能走到相邻的位置，不能跳跃；最后是边界条件：路径必须完整覆盖两段序列，不能只对齐其中一部分。

在这些约束下，DTW 寻找的是一条累计距离最小的路径：

\[ \mathrm{DTW}(X, Y) = \min_{W} \sum_{(i,j)\in W} D(i,j) \]

其中 \(W\) 表示一条合法的对齐路径。直观来说，这条路径描述了“如果允许时间被拉伸或压缩，哪一种对齐方式能让两段序列整体上最相似”。

一个更直观的类比

你可以把 DTW 想象成这样一个过程：两个人分别在地上走出了一串脚印，一个人走得快，脚印之间的间距比较大；另一个人走得慢，脚印密集。如果你要求“第一个人的第 5 个脚印必须对应第二个人的第 5 个脚印”，那几乎不可能对齐。但如果允许某些脚印被“拉开”或“压缩”，只要整体行走方向一致，那么就可以找到一种合理的对应方式。
DTW 正是在做这样一件事情，只不过脚印变成了特征帧，对齐过程被形式化为一条路径搜索问题。

DTW 是否适用于视唱任务？

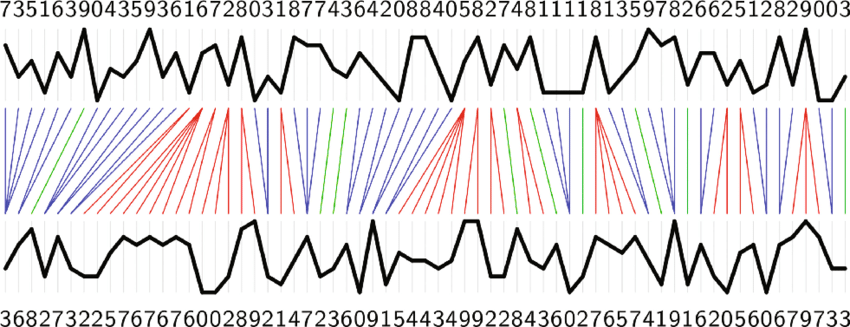
在视唱任务中，一个经常被提出的质疑是：“DTW 这种算法是不是太老了？”但事实上，这并不是问题的关键。DTW 的核心假设非常简单：**两段序列在本质上是相似的，只是时间推进方式不同。**它并不关心音高是否落在标准音级上，也不要求节奏绝对稳定，更不会主动排斥滑音、颤音或不稳定的起音过程。

因此，在视唱任务中，真正决定 DTW 是否“好用”的，并不是算法本身，而是：我们用什么样的方式来描述学生的演唱行为。

一个常见的失败原因

很多“DTW 不适用视唱任务”的结论，往往源自一条隐蔽但致命的逻辑链：学生的演唱行为本身是连续的、波动的、充满不稳定细节的，但我们选用的特征却假设音高是离散、规范、稳定的。结果就是，DTW 被迫在一个已经失真的表示空间中做对齐，最终自然会得出“效果不好”的结论。

这并不是 DTW 的问题，而是在用一把不合适的尺子，去丈量一个本身就不规则的对象。

什么是特征帧（Feature Frame）？

在 DTW 中，“特征帧”并不是一个可有可无的实现细节，而是整个对齐过程的前提条件。DTW 本身并不理解“声音”“旋律”或“音准”，它所能处理的，始终只是一个向量序列。换句话说，DTW 对齐的不是音频，而是你对音频所做出的某种描述。

在形式上，我们通常假设：每隔 \(\Delta t\) 秒，从音频中提取一次特征，用一个 \(d\) 维向量来表示这一小段时间内的声音状态：

\[ x_i \in \mathbb{R}^d \]

其中，\(i\) 是时间索引，\(d\) 是特征维度。一整段音频，最终会被表示为一个随时间变化的向量序列：

\[ X = (x_1, x_2, \dots, x_N) \]

DTW 所做的一切计算，全部发生在这个序列空间中。它既不知道这些向量来自人声，也不知道它们对应的是哪个音符；它唯一能做的事情，是根据你定义的距离度量，判断“第 \(i\) 帧”和“第 \(j\) 帧”到底像不像。

因此，一个非常关键、但经常被忽略的事实是：

DTW 的能力上限，完全由特征帧的表达能力决定。

从“连续声音”到“离散帧”的过程

真实的声音在时间上是连续变化的，而特征帧则是对这一连续过程的离散采样。这个过程本身就隐含了一次“建模假设”：我们默认在 \(\Delta t\) 这么短的时间内，声音的状态是相对稳定的，可以被一个向量近似表示。

你可以把这个过程类比为动画制作：肉眼看到的是连续运动，但动画实际上是由一帧一帧静态画面组成的。每一帧画面保留了哪些信息，直接决定了你能不能还原出原本的动作。
在音频分析中也是一样：特征帧决定了你到底“看到了”声音的哪些方面，又忽略了哪些方面。

特征帧并不只是“特征”，而是一种假设

在很多入门资料中，特征帧常常被介绍为“对音频的压缩表示”，但在 DTW 的语境下，更准确的说法是：每一种特征帧，都隐含了一套关于声音行为的假设。

这些假设包括但不限于：

• 声音的哪些属性是重要的；
• 哪些变化可以忽略；
• 哪些变化应当被视为“错误”；
• 不同时间点之间，什么样的差异是“相似的”。

一旦这些假设与真实的演唱行为不匹配，那么即使 DTW 算法本身完全正确，最终的对齐结果也必然是失败的。

常见特征帧及其隐含假设

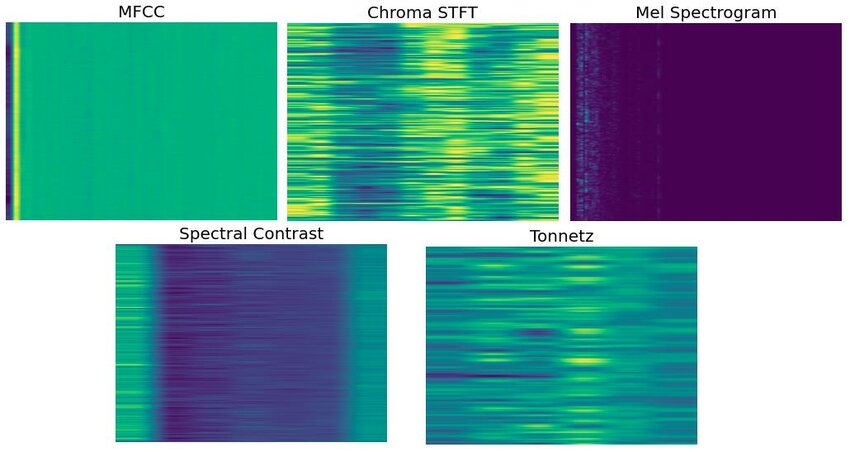
下面我们来看几种在时间序列对齐任务中常见的特征帧，并重点分析它们各自默认了什么样的声音世界观。

MFCC：假设“音色比音高更重要”

MFCC（Mel-Frequency Cepstral Coefficients）的核心目标，是刻画声音的整体频谱形状，其经典计算流程可以写为：

\[ \text{MFCC} = \text{DCT}(\log(\text{MelSpectrum})) \]

从设计初衷上看，MFCC 更关注的是“这个声音听起来像什么”，而不是“这个声音的音高是多少”。它在语音识别中表现优秀，正是因为不同人说同一个词时，音高可能差异很大，但音色和共振结构往往具有一致性。

但在视唱任务中，这种优势反而会变成问题。学生唱得准不准、音程关系是否正确，恰恰是我们最关心的信息，而 MFCC 在计算过程中会主动弱化与绝对音高相关的细节。
结果就是：即使学生整体音高偏移明显，MFCC 序列之间的距离仍然可能很小，从而误导 DTW 认为两段演唱是“相似的”。

Chroma：假设音高是离散且稳定的

Chroma 特征将频率轴压缩到 12 个音级上，其基本形式可以写为：

\[ \text{Chroma}(k) = \sum_{f \in \text{pitch class } k} |X(f)| \]

这种表示方式隐含了一个非常强的前提：在任意时刻，声音都可以被明确地归类到某一个音级上。在乐器演奏、和声分析等任务中，这一假设往往是成立的，因此 Chroma 在这些领域表现良好。

但在学生视唱中，真实情况往往恰恰相反。音高可能在音级之间连续游移，起音阶段不稳定，滑音和颤音频繁出现。在这种情况下，Chroma 特征会在相邻音级之间来回跳动，使得时间序列本身呈现出高度不规则的形态。
DTW 并不知道这是“人类演唱的自然波动”，它只能看到一个不断抖动的离散符号序列。

连续基频（F0）：最贴近真实演唱行为的表示

如果直接使用基频轨迹作为特征帧，那么每一帧可以简单地表示为：

\[ x_i = f_0(t_i) \]

或者进一步转换为音分（cent）尺度：

\[ x_i = 1200 \cdot \log_2\left(\frac{f_0(t_i)}{f_{\text{ref}}}\right) \]

这种表示方式几乎不对音高做任何先验约束。它允许音高连续变化，也允许在目标音附近出现偏差，因此能够自然地表达滑音、颤音、跑音以及不稳定的起音过程。从建模角度看，它与真实演唱行为的距离是最近的。

需要注意的是，F0 表示的问题主要不在于“假设是否合理”，而在于工程层面：噪声干扰、基频估计错误、真假声切换以及无声段的处理，都会对特征序列的稳定性产生影响。但这些问题属于信号处理和系统设计的范畴，而不是 DTW 本身的结构性缺陷。

特征帧与 DTW 的真正关系

在理解了不同特征帧的假设之后，可以回到一个非常重要但经常被忽略的结论：

DTW 并不会修正错误的表示，它只会忠实地对齐你给它的东西。

如果特征帧本身就无法表达学生真实的演唱行为，那么 DTW 只是在一个失真的空间中，寻找“最优但依然错误”的路径。反过来，只要特征允许连续变化和不稳定过程，DTW 反而会成为一种极其自然、几乎符合直觉的时间对齐工具。

小结：真正该问的问题

在视唱任务中，真正值得反复思考的并不是“要不要用 DTW”，而是：“我究竟用什么方式，把学生的演唱行为表示成时间序列？”
DTW 本身并不要求演唱是规范的，它只是尽力对齐你提供的那种表示。当特征允许连续变化和不稳定过程时，DTW 反而是一种非常自然、直观且符合直觉的对齐工具。