概述与直观理解

隐马尔可夫模型（Hidden Markov Model, HMM）是一类用于在“状态不可观测”的情况下，对系统演化过程进行建模和推断的概率模型。它解决的核心问题可以概括为一句话：

当真实世界的状态无法被直接观察时，我们是否仍然能够，仅凭观测到的现象，推断出系统最可能的内部状态变化过程？

为了理解这一点，可以从一个经典且直观的思想实验入手。

假设你被关在一个完全封闭的房间中，永远无法看到外界的天气状况。外面每天的真实天气只可能是三种之一：晴天、阴天或下雨。然而，你每天能够获得的唯一信息，是有人递给你一张纸条，上面记录着某个人当天吃了多少个冰淇淋。

你的目标并不是关心冰淇淋本身，而是希望根据这串“冰淇淋数量”的记录，推断外界每天最可能的天气情况，甚至进一步推断天气是如何随时间变化的。

这正是 HMM 所刻画的典型问题结构。

在这个故事中，天气是真实存在但无法直接观测的，而冰淇淋数量是你唯一能够看到的外显现象。HMM 的建模思想，正是通过对这两层信息之间的统计关系进行刻画，来完成"由现象反推本质"的推断过程。

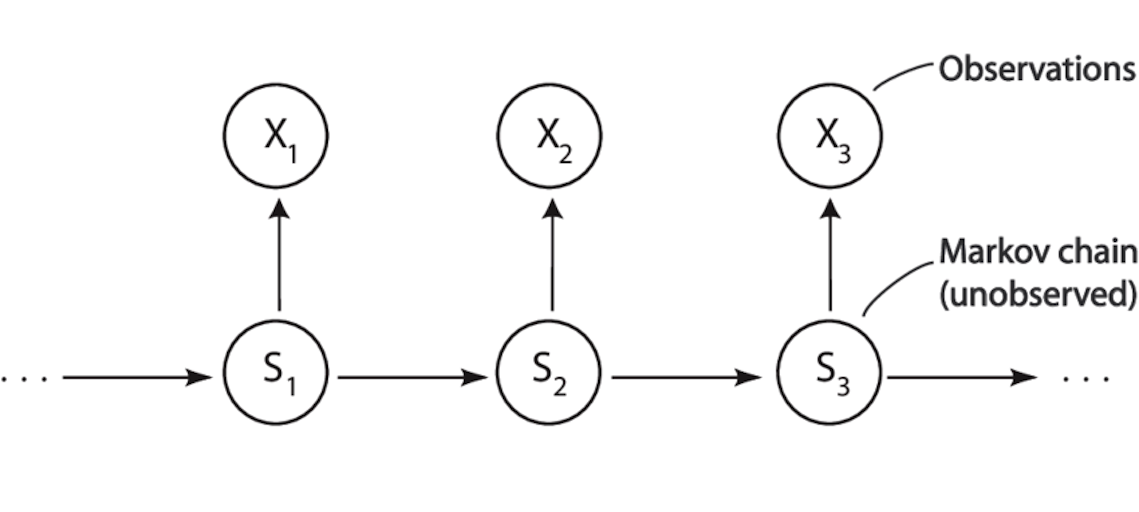
HMM 的三要素结构

一个标准的 HMM 由三类核心要素构成：隐藏状态、观测值以及它们之间的概率规则。

1. 隐藏状态（Hidden States）

隐藏状态描述的是系统在每一个时间点所处的真实内部状态，但这些状态本身是不可被直接观察到的。

在天气—冰淇淋的例子中，隐藏状态集合可以理解为：

晴天、阴天、下雨

这些状态具有两个重要特征：
第一，它们在现实中确实存在，并且随时间发生变化；
第二，它们不会被直接“暴露”给观察者，而只能通过外在行为或现象间接体现出来。

HMM 的建模目标，正是对这条“看不见的状态序列”进行推断。

2. 观测值（Observations）

与隐藏状态相对的是观测值，即在每一个时间点，观察者能够直接获得的数据。

在本例中，观测值就是每天吃掉的冰淇淋数量，例如：

0 个、1 个、2 个

观测值本身并不是我们最终关心的对象，但它们与隐藏状态之间存在统计关联。正是这种关联，使得“从观测推断状态”成为可能。

3. 概率规则：状态如何演化，现象如何产生

HMM 并不试图通过确定性规则去描述世界，而是通过概率来刻画不确定性。这套概率规则只包含两类。

第一类是状态转移概率，用于描述隐藏状态随时间的演化方式。例如：
如果今天是晴天，那么明天仍然是晴天的概率有多大？变成下雨的概率又有多大？

这一假设反映了一个重要事实：现实世界的状态变化通常具有连续性和惯性，而不是完全随机地跳变。这正是“马尔可夫性”的核心含义——未来只依赖于当前状态，而与更久远的历史无关。

第二类是发射概率（观测概率），用于描述在某个隐藏状态下，观察到特定观测值的可能性。例如：
在晴天，人更有可能吃更多冰淇淋；而在下雨天，吃冰淇淋的概率则显著降低。

隐藏状态并不会直接告诉你"我是谁"，它们只会通过观测值"间接露出痕迹"。HMM 正是通过这套概率桥梁，将不可见的状态与可见的现象连接起来。

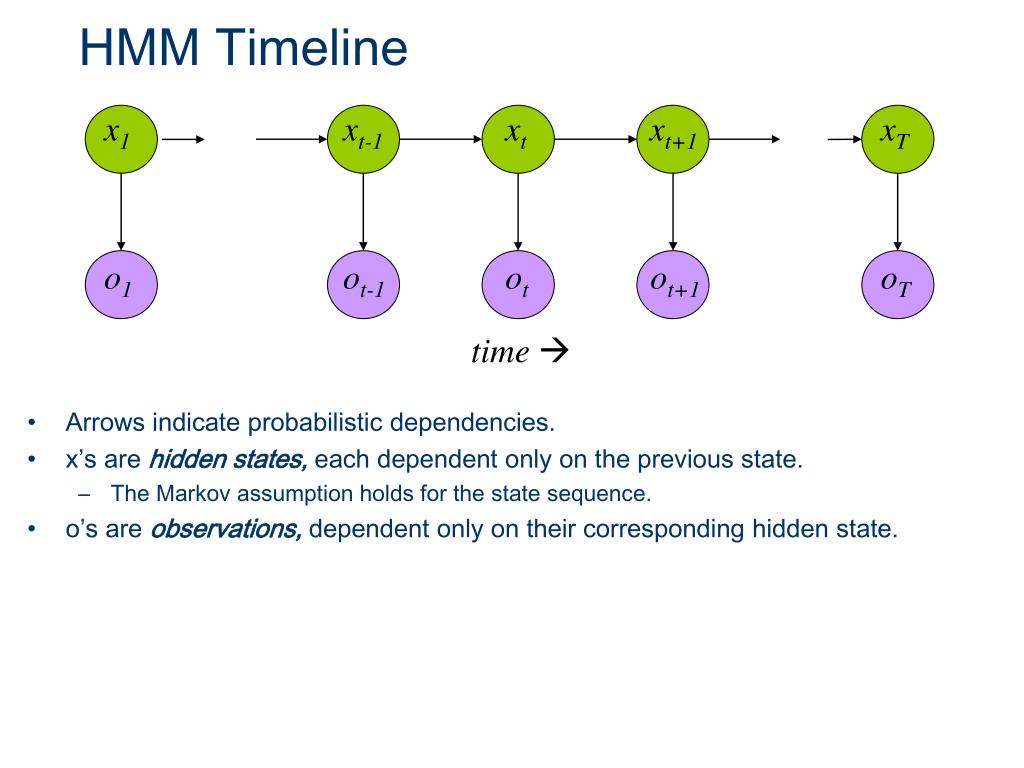
HMM 要解决的三类核心问题

在明确了 HMM 的基本结构之后（隐藏状态、观测变量、转移概率、发射概率等），接下来的核心问题并不是“模型长什么样”，而是：

在这个模型之上，我们究竟能做哪些推断？

几乎所有关于 HMM 的实际应用——无论是语音识别、序列标注，还是时间序列建模——最终都可以归结为三类本质不同、但彼此紧密相关的问题。HMM 的整个算法体系，正是围绕这三类问题建立起来的。

第一类问题：给定模型，观测序列出现的概率是多少？

第一类问题可以表述为：

在模型参数完全已知的前提下，一段观测序列出现的概率有多大？

用数学语言来说，就是在已知模型参数

\[ \lambda = (\pi, A, B) \]

的情况下，计算某一观测序列

\[ O = (o_1, o_2, \dots, o_T) \]

出现的概率：

\[ P(O \mid \lambda) \]

这个问题为什么重要？

乍一看，这个问题似乎有些“被动”，只是算一个概率值，但它实际上是 所有其他推断问题的基础：

• 在语音识别中，它可以用来判断“这个模型是否能很好地解释当前输入的语音”；
• 在模型比较时，它可以作为打分函数，判断多个模型中哪一个更合理；
• 在参数学习（第三类问题）中，它是优化目标函数本身。

难点在哪里？

如果直接暴力计算，你需要枚举 所有可能的隐藏状态序列：

\[ Q = (q_1, q_2, \dots, q_T) \]

而隐藏状态的数量通常是指数级增长的。这意味着，哪怕模型结构很简单，直接枚举也几乎不可行。

对应的算法

为了解决这个“看似简单但计算上极其昂贵”的问题，引入了 前向算法（Forward Algorithm）。

它的核心思想是：
通过动态规划，把“对所有路径求和”的问题，转化为逐时刻的递推计算。

前向算法并不关心“哪条路径最好”，它做的事情只有一件：

把所有可能路径的概率，合理而高效地加在一起。

第二类问题：给定观测序列，最可能的隐藏状态路径是什么？

第二类问题关注的重点发生了变化：

在观测序列已经给定的情况下，哪一条隐藏状态序列最有可能生成这些观测？

数学上，这等价于求解：

\[ \arg\max_Q P(Q \mid O, \lambda) \]

直观理解就是：

“既然这些现象已经发生了，那么幕后最合理的‘状态演化过程’应该是什么？”

这个问题在实际中意味着什么？

这类问题在很多应用中是 真正关心的输出结果：

• 在词性标注中，对应“每个词最可能的词性”；
• 在语音识别中，对应“最可能的音素或状态序列”；
• 在行为建模中，对应“系统在每一时刻最可能处于的内部状态”。

与第一类问题的本质区别

• 第一类问题是 对所有路径求和；
• 第二类问题是 在所有路径中找最大值。

这两者看似相似，但在计算逻辑上是完全不同的任务。

对应的算法

为了解决“找最优路径”的问题，引入了 维特比算法（Viterbi Algorithm）。

它同样使用动态规划，但核心操作不再是“加法”，而是“取最大值”：

• 每一步只保留当前时刻下，到达每个状态的 最优路径；
• 通过记录回溯指针，最终还原整条最优状态序列。

可以把它理解为：
在一张随时间展开的概率图中，寻找一条权重最大的路径。

第三类问题：模型参数未知，能否从数据中反向学习？

前两类问题都有一个重要前提：
模型参数是已知的。

但在真实世界中，这个前提往往并不成立。

于是引出了第三类、也是最具挑战性的问题：

当隐藏状态不可观测、模型参数未知时，是否可以仅凭观测数据，反向估计模型参数？

也就是说，给定一批观测序列：

\[ \{O^{(1)}, O^{(2)}, \dots, O^{(N)}\} \]

我们希望学出最合理的：

\[ \lambda = (\pi, A, B) \]

为什么这个问题困难？

原因在于一个“死循环式”的依赖关系：

• 要估计参数，似乎需要知道隐藏状态；
• 但隐藏状态本身正是我们不知道的。

换句话说：
我们要在“看不见真相”的前提下，学习描述真相的模型。

对应的算法

为了解决这一问题，引入了 Baum–Welch 算法，它本质上是 EM（Expectation–Maximization）算法在 HMM 上的特例。

其核心思想可以概括为两步反复迭代的过程：

1. E 步：在当前参数下，计算“隐藏状态可能是怎样的”（使用前向–后向算法）；
2. M 步：在“期望的隐藏状态分布”基础上，重新估计模型参数。

通过不断重复这两个步骤，模型参数会逐步收敛到一个 局部最优解。

三类问题之间的关系

这三类问题并不是彼此孤立的，而是层层递进、相互依赖的：

• 前向算法是 概率评估的基础工具；
• 维特比算法是 最优路径推断工具；
• Baum–Welch 算法则在内部反复调用前向、后向计算，是 参数学习的核心机制。

理解了这三类问题，也就等于理解了 HMM 的整个推断与学习框架。

模型符号与参数设定

设隐藏状态集合为：

$$ S = \{\text{晴}(S), \text{雨}(R)\} $$

观测集合为：

$$ O = \{0, 1, 2\} $$

初始状态概率定义为：

$$ \pi_i = P(q_1 = i) $$

状态转移概率定义为：

$$ a_{ij} = P(q_{t+1} = j \mid q_t = i) $$

发射概率定义为：

$$ b_j(o) = P(x_t = o \mid q_t = j) $$

一个具体的 HMM 示例

设定初始状态分布为：

$$ \pi_S = 0.6,\quad \pi_R = 0.4 $$

状态转移矩阵为：

$$ A = \begin{bmatrix} 0.7 & 0.3 \\ 0.4 & 0.6 \end{bmatrix} $$

这表示天气具有一定的稳定性，但仍然存在转变的可能。

发射概率如下：

晴天：

$$ b_S(0)=0.1,\quad b_S(1)=0.4,\quad b_S(2)=0.5 $$

雨天：

$$ b_R(0)=0.6,\quad b_R(1)=0.3,\quad b_R(2)=0.1 $$

观测序列

假设连续三天观测到的冰淇淋数量为：

$$ x_{1:3} = [2, 1, 0] $$

Forward（前向算法）

前向算法的目标是计算在当前模型参数下，整段观测序列出现的概率。

其核心思想在于：虽然隐藏状态不可见，但我们可以对所有可能的状态路径进行概率累加。为了避免对路径进行指数级枚举，前向算法采用动态规划进行递推计算。

定义前向变量：

$$ \alpha_t(i) = P(x_{1:t}, q_t = i) $$

它表示在第 \(t\) 天结束时，观测到前 \(t\) 天所有数据，且系统处于状态 \(i\) 的联合概率。

初始化阶段：

$$ \alpha_1(i) = \pi_i \cdot b_i(x_1) $$

代入数值可得：

$$ \alpha_1(S) = 0.30,\quad \alpha_1(R) = 0.04 $$

递推公式为：

$$ \alpha_t(j) = \left( \sum_i \alpha_{t-1}(i)\cdot a_{ij} \right) \cdot b_j(x_t) $$

计算结果为：

$$ \alpha_2(S)=0.0904,\quad \alpha_2(R)=0.0342 $$ $$ \alpha_3(S)=0.007696,\quad \alpha_3(R)=0.028584 $$

最终观测序列的概率为：

$$ P(x_{1:3}) = 0.03628 $$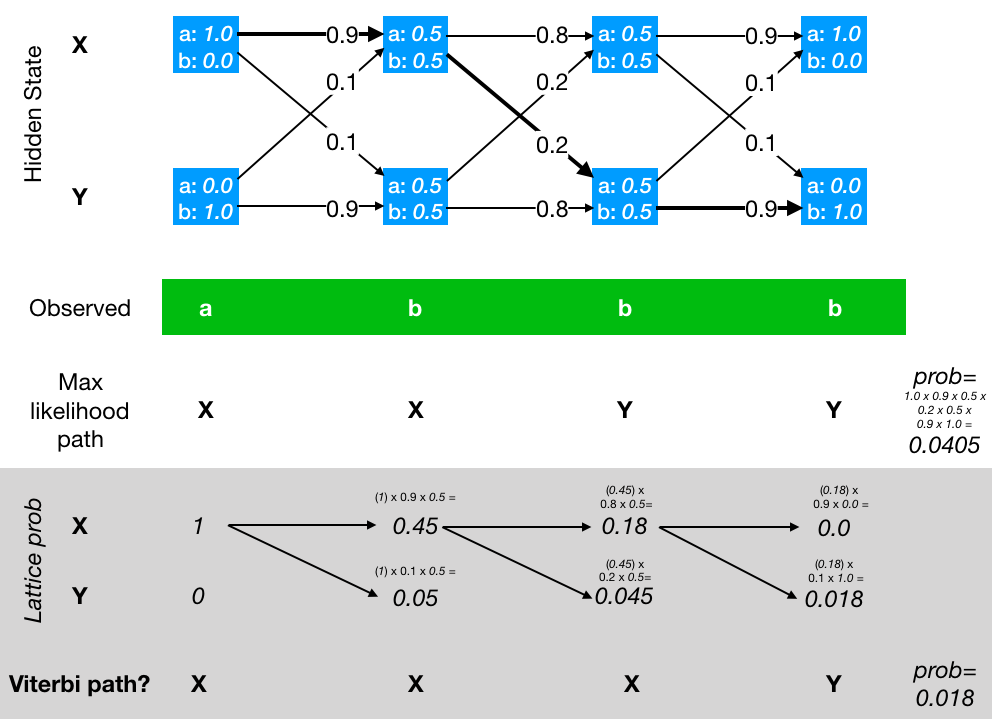

Viterbi（维特比算法）

与前向算法对所有路径求和不同，维特比算法关注的是哪一条隐藏状态路径最可能。

定义最优路径概率：

$$ \delta_t(j) = \max P(q_{1:t-1}, q_t = j, x_{1:t}) $$

并引入回溯指针：

$$ \psi_t(j) = \arg\max \left( \delta_{t-1}(i)\cdot a_{ij} \right) $$

最终回溯得到的最优状态路径为：

$$ [S, S, R] $$

这与直觉高度一致：前两天吃得较多，更符合晴天；最后一天几乎不吃冰淇淋，更符合雨天。

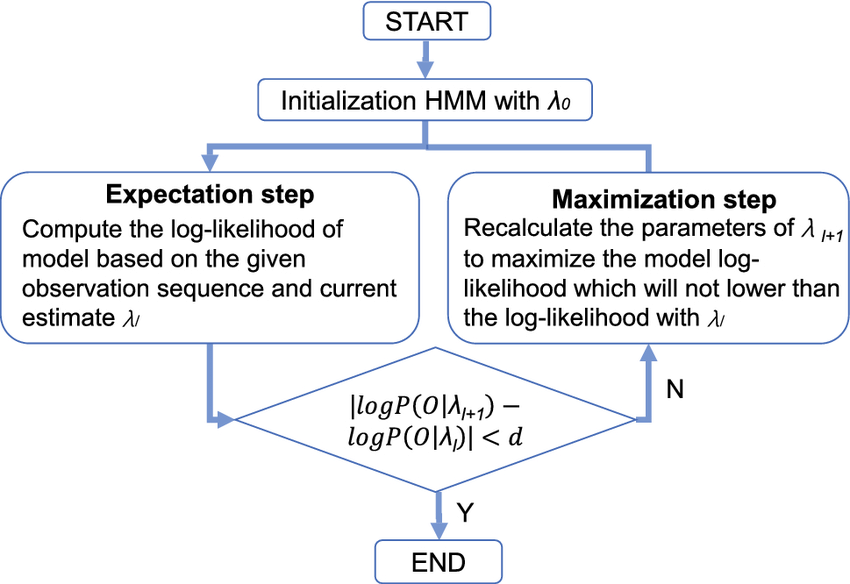
Baum–Welch（EM 训练算法）

当模型参数未知时，可以通过 Baum–Welch 算法从观测数据中自动估计这些参数。该算法是 EM 框架在 HMM 上的具体实现。

其核心思想是交替进行两步：

E 步，在当前模型下估计每个时间点属于各个隐藏状态的概率； M 步，利用这些"软统计结果"重新更新模型参数。

后向变量定义为：

$$ \beta_t(i) = P(x_{t+1:T} \mid q_t = i) $$

状态后验概率为：

$$ \gamma_t(i) = \frac{\alpha_t(i)\beta_t(i)} {\sum_k \alpha_t(k)\beta_t(k)} $$

参数更新公式如下：

$$ \pi_i \leftarrow \gamma_1(i) $$ $$ a_{ij} \leftarrow \frac{\sum_{t=1}^{T-1} \xi_t(i,j)} {\sum_{t=1}^{T-1} \gamma_t(i)} $$ $$ b_j(o) \leftarrow \frac{\sum_{t: x_t=o} \gamma_t(j)} {\sum_{t=1}^{T} \gamma_t(j)} $$

小结

从整体上看，隐马尔可夫模型并不是由某一个“孤立的算法”构成的，而是围绕着“如何在不可观测的世界中进行推断”这一核心目标，形成了一套彼此配合、逻辑闭合的算法体系。

前向算法解决的是概率评估问题。在模型参数已知的前提下，它回答的是：“当前模型对这段观测数据的解释能力有多强？”这一问题本身并不直接给出路径或决策结果，但它为模型比较、模型选择以及参数学习提供了最基础的量化依据。可以说，前向算法定义了“什么叫做一个模型在概率意义上是合理的”。

维特比算法关注的则是结构性解释问题。在观测序列已经发生这一既定事实下，它不再关心所有可能性的总体概率，而是试图给出一条最具代表性的隐藏状态演化路径。它提供的是一种“单一路径层面的解释”，使得 HMM 不仅能回答“有多可能”，还能回答“最可能是怎样发生的”。

而 Baum–Welch 算法进一步将视角从“推断”推进到了“学习”。在隐藏状态完全不可观测的现实条件下，它通过反复估计隐藏状态的期望分布，并据此更新模型参数，使得 HMM 可以仅依赖观测数据完成自我调整与优化。这一过程使模型从静态假设，转变为能够随数据不断修正的动态系统。

从逻辑关系上看，这三类算法并非并列存在，而是层层递进、相互依赖的：
前向（及后向）算法提供了对隐藏状态不确定性的概率刻画；
维特比算法在此基础上给出最优解释路径；
Baum–Welch 算法则反复调用概率评估结果，实现参数层面的学习。

正是这三者的协同作用，使得隐马尔可夫模型不仅“形式上完整”，而且在推断、解释与学习三个层面上形成了一个自洽且可操作的统一框架。